已知函数$y=\frac{{|{{x^2}+x-2}|}}{x-1}$与函数y=kx-2的图象恰有两个交点.则实数k的取值范围是．题目和参考答案——青夏教育精英家教网——

题目内容

17．已知函数$y=\frac{{|{{x^2}+x-2}|}}{x-1}$与函数y=kx-2的图象恰有两个交点，则实数k的取值范围是（-1，1）∪（1，5）．

分析化简函数的解析式，画出两个函数的图象，判断k的范围即可．

解答解：$f（x）=\frac{{|{（x+2）（x-1）}|}}{x-1}=\left\{\begin{array}{l}-x-2，-2≤x＜1\\ x+2，x＜-2或x＞1.\end{array}\right.$
直线y=kx-2过定点（0，-2），
由函数图象：
可知结果为：（-1，1）∪（1，5）．
给答案为：（-1，1）∪（1，5）．

点评本题考查函数与方程的应用，函数的零点个数的判断，考查数形结合思想的应用．

练习册系列答案

智趣暑假温故知新系列答案

考点分类集训期末复习暑假作业系列答案

导学练暑假作业系列答案

快乐暑假假期作业云南人民出版社系列答案

英语小英雄天天默写系列答案

英才园地系列答案

暑假作业安徽少年儿童出版社系列答案

胜券在握打好基础作业本系列答案

暑假作业二十一世纪出版社系列答案

阳光作业暑假乐园系列答案

相关题目

7．已知复数z满足（3-i）z=2+i（i为虚数单位），则z的共轭复数是（　　）

$\frac{1}{2}$+$\frac{1}{2}$i

$\frac{1}{2}$-$\frac{1}{2}i$

-$\frac{1}{2}$+$\frac{1}{2}$i

-$\frac{1}{2}$-$\frac{1}{2}$i

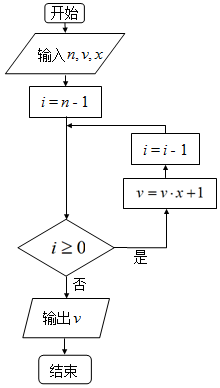我国南宋时期的数学家秦九韶（约1202-1261）在他的著作《数书九章》中提出了多项式求值的秦九韶算法．如图所示的框图给出了利用秦九韶算法求多项式的一个实例．若输入的n=5，v=1，x=2，则程序框图计算的是（　　）

	A．	2⁵+2⁴+2³+2²+2+1		B．	2⁵+2⁴+2³+2²+2+5
	C．	2⁶+2⁵+2⁴+2³+2²+2+1		D．	2⁴+2³+2²+2+1

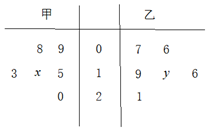如图茎叶图记录了甲，乙两班各六名同学一周的课外阅读时间（单位：小时），已知甲班数据的平均数为13，乙班数据的中位数为17，那么x的位置应填3；y的位置应填8．

12．已知椭圆E：mx²+y²=1（m＞0）．
（Ⅰ）若椭圆E的右焦点坐标为$（\sqrt{3}，0）$，求m的值；
（Ⅱ）由椭圆E上不同三点构成的三角形称为椭圆的内接三角形．若以B（0，1）为直角顶点的椭圆E的内接等腰直角三角形恰有三个，求m的取值范围．

2．已知函数f（x）=xsinx+cosx．
（1）当$x∈（\frac{π}{4}，π）$时，求函数f（x）的单调区间；
（2）若存在$x∈（\frac{π}{4}，\frac{π}{2}）$，使得f（x）＞kx²+cosx成立，求实数k的取值范围．

9．在凸四边形ABCD中，BD=2，且$\overrightarrow{AC}•\overrightarrow{BD}=0$，$（\overrightarrow{AB}+\overrightarrow{DC}）•（\overrightarrow{BC}+\overrightarrow{AD}）=5$，则四边形ABCD的面积为3．

13．若数列{a_n}为等差数列，S₉₉=198，则a₄₈+a₄₉+a₅₀+a₅₁+a₅₂=（　　）

14．若圆x²+y²-4x-4y-10=0上至少有三个不同的点到直线l：y=x+b的距离为$2\sqrt{2}$，则b取值范围为[-2，2]．