题目内容
13.(普通中学做)已知数列{an}为等差数列,a3=3,a7=7,数列{bn}的前n项和为Sn,且Sn=2bn-2(1)求{an}、{bn}的通项公式
(2)若cn=$\frac{{a}_{n}}{{b}_{n}}$,数列{cn}的前n项和为Tn,求Tn.
分析 (1)利用等差数列通项公式列出方程组,求出首项、公差,由此能求出{an}的通项公式,由数列{bn}的前n项和Sn=2bn-2,得{bn}是首项为2,公比为2的等比数列,由此能求出{bn}的通项公式.
(2)由cn=$\frac{{a}_{n}}{{b}_{n}}$=$\frac{n}{{2}^{n}}$,利用错位相减法能求出数列{cn}的前n项和.
解答 解:(1)∵数列{an}为等差数列,a3=3,a7=7,设公差为d.
∴$\left\{\begin{array}{l}{{a}_{1}+2d=3}\\{{a}_{1}+6d=7}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=1}\end{array}\right.$,
∴an=1+(n-1)×1=n,n∈N*.
∵数列{bn}的前n项和为Sn,且Sn=2bn-2,
∴b1=S1=2b1-2,解得b1=2,
当n≥2时,由Sn=2bn-2及Sn-1=2bn-1-2,
两式相减,得bn=2bn-2bn-1,∴bn=2bn-1,
∴{bn}是首项为2,公比为2的等比数列,
∴bn=2•2n-1=2n.(n∈N*).
(2)∵cn=$\frac{{a}_{n}}{{b}_{n}}$=$\frac{n}{{2}^{n}}$,
∴数列{cn}的前n项和:
Tn=$\frac{1}{2}+\frac{2}{{2}^{2}}+…+\frac{n}{{2}^{n}}$,①
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}+…+\frac{n}{{2}^{n+1}}$,②
①-②,得:$\frac{1}{2}{T}_{n}$=$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$
=1-$\frac{n+2}{{2}^{n+1}}$,
∴Tn=2-$\frac{n+2}{{2}^{n}}$.
点评 本题考查数列的通项公式及前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

| A. | $\frac{15}{2}$ | B. | $\frac{13}{2}$ | C. | $\frac{31}{2}$ | D. | $\frac{51}{2}$ |
| A. | $\frac{\sqrt{13}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | -$\frac{\sqrt{3}}{4}$ | D. | -$\frac{\sqrt{13}}{4}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
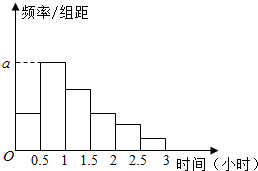 随着智能手机等电子产品的普及,“低头族”正成为现代社会的一个流行词.在路上、在餐厅里、在公交车上,随处可见低头玩手机的人,这种“低头族现象”冲击了人们面对面交流的温情,也对人们的健康构成一定的影响.为此,某报社发起一项专题调查,记者随机采访了M名市民,得到这M名市民每人在一天内低头玩手机的时间(单位:小时),根据此数据作出频数的统计表和频率分布直方图如下:
随着智能手机等电子产品的普及,“低头族”正成为现代社会的一个流行词.在路上、在餐厅里、在公交车上,随处可见低头玩手机的人,这种“低头族现象”冲击了人们面对面交流的温情,也对人们的健康构成一定的影响.为此,某报社发起一项专题调查,记者随机采访了M名市民,得到这M名市民每人在一天内低头玩手机的时间(单位:小时),根据此数据作出频数的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [0,0.5) | 4 | 0.10 |
| [0.5,1) | m | p |
| [1,1.5) | 10 | n |
| [1.5,2) | 6 | 0.15 |
| [2,2.5) | 4 | 0.10 |
| [2.5,3) | 2 | 0.05 |
| 合计 | M | 1 |
(Ⅱ)试估计这M名市民在一天内低头玩手机的平均时间(同一组的数据用该组的中间值作代表);
(Ⅲ)在所取样本中,从一天内低头玩手机的时间不少于2小时的市民中任取2人,求两人在一天内低头玩手机的时间都在区间[2,2.5)内的概率.
 如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上的一点(含端点),则$\overrightarrow{AD}$•$\overrightarrow{BC}$的取值范围是[-3,0].
如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上的一点(含端点),则$\overrightarrow{AD}$•$\overrightarrow{BC}$的取值范围是[-3,0].