题目内容
6.观察下列等式(1+x+x2)1=1+x+x2,
(1+x+x2)2=1+2x+3x2+2x3+x4,
(1+x+x2)3=1+3x+6x2+7x3+6x4+3x5+x6,
(1+x+x2)4=1+4x+10x2+16x3+19x4+16x5+10x6+4x7+x8,
…
由以上等式推测对于n∈N*,若(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,则a2=$\frac{n(n+1)}{2}$.
分析 本题考查的知识点是归纳推理,我们可以根据已知条件中的等式,分析等式两边的系数及指数部分与式子编号之间的关系,易得等式右边展开式中的第三项分别为:1,3,6,10,…,归纳后即可推断出a2的等式.
解答 解:由已知中的式了,我们观察后分析:
等式右边展开式中的第三项分别为:1,3,6,10,…,
即:1,1+2.1+2+3,1+2+3+4,…
根据已知可以推断:
第n(n∈N*)个等式中a2为:1+2+3+4+…+n=$\frac{n(n+1)}{2}$.
故答案为:$\frac{n(n+1)}{2}$.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
1.已知集合M={x|x2≥1},则集合∁RM=( )
| A. | {x|-1<x<1} | B. | {x|-1≤x≤1} | C. | {x|x<-1或x>1} | D. | {x|x≤-1或x≥1} |
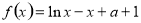 .
.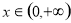 使得
使得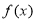 ≥0成立,求
≥0成立,求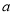 的范围;
的范围;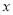 >1时,在(1)的条件下,
>1时,在(1)的条件下,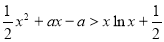 成立.
成立.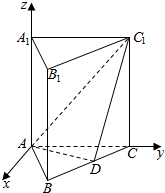 已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).
已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).