题目内容
15.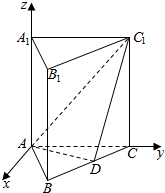 已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).
已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).
分析 根据题意,利用空间直角坐标系中三棱柱的边角关系,写出点D的坐标,
再根据平面法向量的定义列出方程组求出平面的一个法向量.
解答 解:在空间直角坐标系A-xyz中,A(0,0,0),C(0,1,0),
A1(0,0,1),C1(0,1,1);
由AD⊥C1D,得出AD⊥侧面BCC1B1,
∴AD⊥BC,D为BC的中点,
∴点D的坐标为($\frac{\sqrt{3}}{2}$cos60°,$\frac{\sqrt{3}}{2}$sin60°,0),
即($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0);
设平面ADC1的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{{AC}_{1}}$=(0,1,1),$\overrightarrow{AD}$=($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{AC}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{AD}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{y+z=0}\\{\frac{\sqrt{3}}{4}x+\frac{3}{4}y=0}\end{array}\right.$,
令y=-1,得z=1,x=$\sqrt{3}$,
∴法向量$\overrightarrow{n}$=($\sqrt{3}$,-1,1).
故答案为:($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),($\sqrt{3}$,-1,1).
点评 本题考查了空间直角坐标系的应用问题,也考查了利用坐标法求平面的法向量问题,是综合性题目.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | (-∞,3) | B. | (3,+∞) | C. | (-∞,4) | D. | (4,+∞) |
| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 2$\sqrt{2}$ |