题目内容
11.函数y=2x+1的值域为(1,+∞),函数y=$\frac{1}{{2}^{x}-1}$的值域为(-∞,-1)∪(0,+∞).分析 由题意知2x>0,从而确定2x+1与$\frac{1}{{2}^{x}-1}$的取值范围,从而解得.
解答 解:∵2x>0,
∴2x+1>1,
∴函数y=2x+1的值域为(1,+∞);
∵2x-1>-1且2x-1≠0,
∴$\frac{1}{{2}^{x}-1}$<-1或$\frac{1}{{2}^{x}-1}$>0;
故函数y=$\frac{1}{{2}^{x}-1}$的值域为(-∞,-1)∪(0,+∞);
故答案为:(1,+∞),(-∞,-1)∪(0,+∞).
点评 本题考查了函数的值域的求法与应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.一个质点从原点出发,每秒末必须向右、或向左、或向上、或向下跳一个单位长度.则此质点在第8秒末到达点P(4,2)的跳法共有( )
| A. | 98 | B. | 448 | C. | 1736 | D. | 196 |
19.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x},x≤1}\\{-x+4,x>1}\end{array}\right.$;若f(x)=2,则x=2或log32.
2.设F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两个焦点,P在双曲线上,若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=2ac(c=$\sqrt{{a}^{2}+{b}^{2}}$),则双曲线的离心率为( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | 2 | D. | $\frac{\sqrt{5}+1}{2}$ |
17.过抛物线C:y2=2x的焦点F,且斜率为k(k>0)的直线l交C于R,S两点,若$\overrightarrow{RF}$=2$\overrightarrow{FS}$,则k的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 2$\sqrt{2}$ |
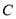
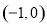 ,以
,以 为圆心的圆与直线
为圆心的圆与直线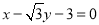 相切.
相切.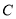 的方程;
的方程;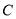 上存在两点关于直线
上存在两点关于直线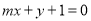 对称,求
对称,求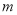 的值.
的值.