题目内容
20.设数列{an}的前n项和为Sn,己知a1=l,nan+1=(n+2)Sn,n∈N*.(1)求证:$\{\frac{S_n}{n}\}$是等比数列;
(2)设Tn=S1+S2+…+Sn,求证:(n+l) Tn<nSn+1.
分析 (1)由题意可知:n(Sn+1-Sn)=(n+2)Sn,则$\frac{{S}_{n+1}}{n+1}$=2$\frac{{S}_{n}}{n}$,则数列$\{\frac{S_n}{n}\}$是以1为首项,2为公比的公比的等比数列;
(2)由(1)可知:Sn=n•2n-1,Tn=S1+S2+…+Sn=1•20+2•21+…+n•2n-1,则2Tn=1•21+2•22+…+(n-1)•2n-1+n•2n,两式相减即可求得:Tn=(n-1)•2n+1,利用作差法(n+l) Tn-nSn+1=(n+1)(1-2n)<0,即可证明(n+l) Tn<nSn+1.
解答 (1)证明:由题意可知:nan+1=(n+2)Sn,则:n(Sn+1-Sn)=(n+2)Sn,
∴nSn+1=(n+1)Sn,即$\frac{{S}_{n+1}}{n+1}$=2$\frac{{S}_{n}}{n}$,
由$\frac{{S}_{1}}{1}$=1,
∴数列$\{\frac{S_n}{n}\}$是以1为首项,2为公比的公比的等比数列;
(2)证明:由(1)可知:$\frac{{S}_{n}}{n}$=1•2n-1=2n-1,则Sn=n•2n-1,
Tn=S1+S2+…+Sn,
∴Tn=1•20+2•21+…+n•2n-1,
则2Tn=1•21+2•22+…+(n-1)•2n-1+n•2n,
两式相减可得:-Tn=1+2+22+…+2n-1-n•2n,
=$\frac{1(1-{2}^{n})}{1-2}$-n•2n,
=2n-1-n•2n,
=(1-n)•2n-1,
Tn=(n-1)•2n+1,
(n+l) Tn-nSn+1=(n2-1)2n+(n+1)-n(n+1)2n=(n+1)(1-2n),
由n∈N*,
∴n+1>0,1-2n<0,
∴(n+1)(1-2n)<0,
∴(n+l) Tn<nSn+1.
点评 本题考查等比数列的证明,等比数列通项公式及前n项和公式,考查“错位相减法”求数列的前n项和,考查作差法比较多项式的大小,考查计算能力,属于中档题.

| A. | 96个 | B. | 108个 | C. | 120个 | D. | 216个 |
| A. | $\frac{20}{3}$ | B. | $\frac{42}{5}$+2$\sqrt{2}$ | C. | $\frac{136}{15}$ | D. | $\frac{27}{5}$+2$\sqrt{2}$ |
| A. | 1+$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 1 |
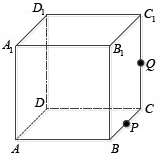 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).