题目内容
11.在长方体ABCD-A1B1C1D1中,若AB=BC=1,AA1=$\sqrt{2}$,则异面直线BD1与CC1所成角的大小为$\frac{π}{4}$.分析 根据条件画出图形,并连接D1B1,可以判断出∠B1BD1为异面直线BD1与CC1所成的角,从而在Rt△BB1D1中可求出cos∠B1BD1,进而便可得出∠B1BD1的大小.
解答 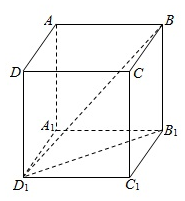 解:如图,连接D1B1;
解:如图,连接D1B1;
∵CC1∥BB1;
∴BD1与CC1所成角等于BD1与BB1所成角;
∴∠B1BD1为异面直线BD1与CC1所成角;
∴在Rt△BB1D1中,cos∠B1BD1=$\frac{B{B}_{1}}{B{D}_{1}}=\frac{\sqrt{2}}{\sqrt{1+1+2}}=\frac{\sqrt{2}}{2}$;
∴异面直线BD1与CC1所成角的大小为$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 考查异面直线及异面直线所成角的概念,三角函数的定义,已知三角函数值求角.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
19.行列式$|\begin{array}{l}{1}&{4}&{7}\\{2}&{5}&{8}\\{3}&{6}&{9}\end{array}|$中,元素7的代数余子式的值为( )
| A. | -15 | B. | -3 | C. | 3 | D. | 12 |
6.设θ是两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角,若对任意实数t,|$\overrightarrow{a}$+t$\overrightarrow{b}$|的最小值为1,则下列判断正确的是( )
| A. | 若|$\overrightarrow{a}$|确定,则θ唯一确定 | B. | 若|$\overrightarrow{b}$|确定,则θ唯一确定 | ||
| C. | 若θ确定,则|$\overrightarrow{b}$|唯一确定 | D. | 若θ确定,则|$\overrightarrow{a}$|唯一确定 |
3.在等比数列{an}中,a2=1,a6=9,则a4=( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $±\sqrt{3}$ |
1.已知2x1+1,2x2+1,2x3+1,…,2xn+1的方差是3,则x1,x2,x3,…,xn的标准差为( )
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 3 | D. | $\sqrt{3}$ |