题目内容
12.已知实数x、y满足条件:$\left\{\begin{array}{l}x-y-1≤0\\ 2x+y-4≥0\\ y≤2\end{array}\right.$,则$\frac{2x^2+y^2}{xy}$的最大值与最小值的和为( )| A. | $\frac{20}{3}$ | B. | $\frac{42}{5}$+2$\sqrt{2}$ | C. | $\frac{136}{15}$ | D. | $\frac{27}{5}$+2$\sqrt{2}$ |
分析 令$\frac{y}{x}$=k,由线性规划求得:$\frac{2}{5}$≤k≤2,将$\frac{2x^2+y^2}{xy}$变形为$\frac{2x}{y}$+$\frac{y}{x}$=$\frac{2}{k}$+k,则易求$\frac{2x^2+y^2}{xy}$的最大值与最小值.
解答 解:由约束条件$\left\{\begin{array}{l}x-y-1≤0\\ 2x+y-4≥0\\ y≤2\end{array}\right.$,作出可行域如图,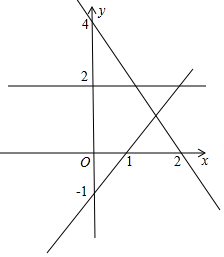
令$\frac{y}{x}$=k,由线性规划得到:$\frac{2}{5}$≤k≤2,
令z=$\frac{2x^2+y^2}{xy}$=$\frac{2x}{y}$+$\frac{y}{x}$=$\frac{2}{k}$+k.
当k=$\frac{2}{5}$时,zmin=$\frac{27}{5}$,zmax=2$\sqrt{2}$,
则$\frac{2x^2+y^2}{xy}$的最大值与最小值的和为:$\frac{27}{5}$+2$\sqrt{2}$,
故选:D.
点评 本题主要考查线性规划的应用,确定平面区域的位置,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
3.在等比数列{an}中,a2=1,a6=9,则a4=( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $±\sqrt{3}$ |
7.在△OAB中,已知OA=5,OB=4,点P是AB的中点,则$\overrightarrow{OP}•\overrightarrow{AB}$=( )
| A. | 10 | B. | -$\frac{9}{2}$ | C. | 20 | D. | -20 |
1.已知2x1+1,2x2+1,2x3+1,…,2xn+1的方差是3,则x1,x2,x3,…,xn的标准差为( )
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 3 | D. | $\sqrt{3}$ |
2.已知△ABC是边长为a的正三角形,那么△ABC平面直观图△A′B′C′的面积为( )
| A. | $\frac{\sqrt{6}}{16}$a2 | B. | $\frac{\sqrt{3}}{32}$a2 | C. | $\frac{\sqrt{3}}{16}$a2 | D. | $\frac{\sqrt{6}}{8}$a2 |