题目内容
15.从集合{1,2,3,4,5,6,7)中任取五个不同元素构成数列al,a2,a3,a4,a5,其中a3是al和a5的等差中项,且a2<a4,则这样的数列共有( )| A. | 96个 | B. | 108个 | C. | 120个 | D. | 216个 |
分析 a3是a1和a5的等差中项,可得2a3=a1+a5,从集合{1,2,3,4,5,6,7}中任取五个不同元素,其中3个满足a3是a1和a5的等差中项的共有18组:1,2,3;3,2,1;….其中对于每一组等差数列,且a2<a4的可有:${C}_{4}^{2}$=6组满足.即可得出.
解答 解:∵a3是a1和a5的等差中项,
∴2a3=a1+a5,
从集合{1,2,3,4,5,6,7}中任取五个不同元素,
其中3个满足a3是a1和a5的等差中项的共有18组:1,2,3;3,2,1;1,3,5;5,3,1;1,4,7;7,4,1;2,3,4;4,3,2;2,4,6;6,4,2;3,4,5;5,4,3;3,5,7;7,5,3;4,5,6;6,5,4;5,6,7;7,6,5.
其中对于每一组等差数列,且a2<a4的可有:${C}_{4}^{2}$=6组满足.
∴这样的数列共有18×6=108组.
故选:B.
点评 本题考查了等差数列的性质、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设θ是两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角,若对任意实数t,|$\overrightarrow{a}$+t$\overrightarrow{b}$|的最小值为1,则下列判断正确的是( )
| A. | 若|$\overrightarrow{a}$|确定,则θ唯一确定 | B. | 若|$\overrightarrow{b}$|确定,则θ唯一确定 | ||
| C. | 若θ确定,则|$\overrightarrow{b}$|唯一确定 | D. | 若θ确定,则|$\overrightarrow{a}$|唯一确定 |
3.在等比数列{an}中,a2=1,a6=9,则a4=( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $±\sqrt{3}$ |
7.在△OAB中,已知OA=5,OB=4,点P是AB的中点,则$\overrightarrow{OP}•\overrightarrow{AB}$=( )
| A. | 10 | B. | -$\frac{9}{2}$ | C. | 20 | D. | -20 |
5.直线ax+2y=0平行于直线x+y=1,则a等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
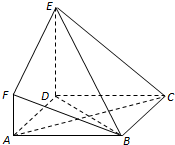 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.