题目内容
若点P(x,y)满足线性约束条件
,则z=x-y的最小值是 ;u=
的取值范围是 .
|
| y+1 |
| x-1 |
考点:简单线性规划
专题:不等式的解法及应用
分析:画出满足条件的平面区域,由z=x-y得:y=x-z,当直线过(-2,0)时,z最小,u=
表示过平面区域的点(x,y)与(1,-1)的直线的斜率,通过图象即可得出.
| y+1 |
| x-1 |
解答:
解:画出满足条件的平面区域,
如图示:
 ,
,
由z=x-y得:y=x-z,当直线过(-2,0)时,
z最小,Z最小值=-2,
u=
表示过平面区域的点(x,y)与(1,-1)的直线的斜率,
显然直线过(-2,0)时,u=-
,
直线过(
,
)时,u=-7,
故答案为:-2,[-7,-
].
如图示:
 ,
,由z=x-y得:y=x-z,当直线过(-2,0)时,
z最小,Z最小值=-2,
u=
| y+1 |
| x-1 |
显然直线过(-2,0)时,u=-
| 1 |
| 3 |
直线过(
| 2 |
| 3 |
| 4 |
| 3 |
故答案为:-2,[-7,-
| 1 |
| 3 |
点评:本题考查了简单的线性规划问题,考查了数形结合思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设全集U={x|log2x<3},A={x|1<2x<32},则CUA=( )
| A、(-∞,0]∪[5,8) |
| B、(-∞,0]∪(5,8) |
| C、[5,8) |
| D、(5,8) |
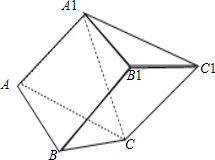 已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2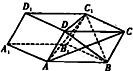 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2