Question

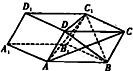已知四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是边长为2

3

的正方形，平面ACC₁⊥ABCD，BC₁=CC₁，直线DB与平面BCC₁B₁成30°角，
（1）求证：平面BC₁D⊥平面ABCD；
（2）求四棱柱ABCD-A₁B₁C₁D₁的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,平面与平面垂直的判定

专题：空间位置关系与距离

分析：（1）设AC，BD交于点O，连结C₁O，取BC中点E，AB中点F，连结C₁E，OE，C₁F，OF，由已知得BC⊥C₁O，再由平面ACC₁⊥ABCD，得C₁O⊥平面ABCD，由此能证明平面BC₁D⊥平面ABCD．
（2）以O为原点，OA为x轴，OB为y轴，OC₁为z轴，建立空间直角坐标系，利用向量法能求出四棱柱ABCD-A₁B₁C₁D₁的体积．

解答： （1）证明：设AC，BD交于点O，连结C₁O，
取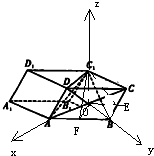BC中点E，AB中点F，连结C₁E，OE，C₁F，OF，
∵四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是边长为2

3

的正方形，
平面ACC₁⊥ABCD，BC₁=CC₁，
∴C₁E⊥BC，OE⊥BC，OF⊥AB，
又OE∩∩C₁E=E，∴BC⊥平面C₁OE，∴BC⊥C₁O，
∵OF∥BC，∴OF⊥C₁O，
∵平面ACC₁⊥ABCD，∴C₁O⊥平面ABCD，
∵C₁O?平面BC₁D，∴平面BC₁D⊥平面ABCD．
（2）解：以O为原点，OA为x轴，OB为y轴，OC₁为z轴，
建立空间直角坐标系，
∵ABCD是边长为2

3

的正方形，设OC₁=t，
则B（0，

3

，0），D（0，-

3

，0），C₁（0，0，t），C（-

3

，0，0），

BD

=（0，-2

3

，0），

BC1

=（0，-

3

，t），

BC

=（-

3

，-

3

，0），
设平面BCC₁的法向量

n

=（x，y，z），
则

n • BC1 =- 3 y+tz=0 n • BC =- 3 x- 3 y=0

，取x=1，得

n

=（1，-1，-

3

t

），
∵直线DB与平面BCC₁B₁成30°角，
∴sin30°=|cos＜

n

，

BD

＞|=|

2 3

2 3 • 2+ 3 t2

|=

1

2

，
解得t=

6

2

或t=-

6

2

（舍）
∴C1O=

6

2

，
∴S_{正方形ABCD}=2

3

×2

3

=12，
∴四棱柱ABCD-A₁B₁C₁D₁的体积V=S_{正方形ABCD}×C₁O=12×

6

2

=6

6

．

点评：本题考查平面与平面垂直的证明，考查四棱柱的体积的求法，解题时要认真审题，注意空间思维能力的培养．