题目内容
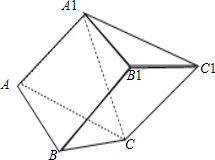 已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2| 3 |
(1)求侧棱A1A与底面ABC所成角的大小;
(2)求侧面A1ABB1与底面ABC所成二面角的大小.
考点:二面角的平面角及求法,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)由已知得直线AA1在底面ABC内的射影为直线AC,∠A1AC为侧棱AA1与底面ABC所成的角,由此能求出侧棱A1A与底面ABC所成角的大小.
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1,由已知得∠A1NM即为所求二面角的平面角,由此能求出侧面A1ABB1与底面ABC所成二面角的大小.
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1,由已知得∠A1NM即为所求二面角的平面角,由此能求出侧面A1ABB1与底面ABC所成二面角的大小.
解答:
解:(1)因为侧面A1ACC1⊥底面ABC,AA1?侧面A1ACC1,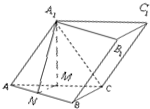
侧面A1ACC1∩底面ABC=AC
所以直线AA1在底面ABC内的射影为直线AC
故∠A1AC为侧棱AA1与底面ABC所成的角
又AA1⊥A1C,AA1=A1C,
所以∠A1AC=45°为所求.
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1
由(1)知A1M⊥AC,
故A1M⊥底面ABC,A1M⊥AB
又MN∥BC,∠ABC=90°
所以MN⊥AB,又MN∩A1M=M,所以AB⊥平面A1MN
则∠A1NM即为所求二面角的平面角
在RtA1MN中,A1M=
,AC=3,MN=
BC=1,∠A1MN=90°,
所以tan∠A1MN=
=3,∠A1MN=arctan3.
即所求二面角的大小为arctan3.

侧面A1ACC1∩底面ABC=AC
所以直线AA1在底面ABC内的射影为直线AC
故∠A1AC为侧棱AA1与底面ABC所成的角
又AA1⊥A1C,AA1=A1C,
所以∠A1AC=45°为所求.
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1
由(1)知A1M⊥AC,
故A1M⊥底面ABC,A1M⊥AB
又MN∥BC,∠ABC=90°
所以MN⊥AB,又MN∩A1M=M,所以AB⊥平面A1MN
则∠A1NM即为所求二面角的平面角
在RtA1MN中,A1M=
| ||
| 2 |
| 1 |
| 2 |
所以tan∠A1MN=
| A1M |
| MN |
即所求二面角的大小为arctan3.
点评:本题考查直线与平面所成角的大小的求法,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
i是虚数单位,复数z=
在复平面内对应的点在第三象限,则实数k的范围是( )
| k-i |
| i |
| A、k≥0 | B、k>0 |
| C、k≤0 | D、k<0 |
设抛物线y2=2px(p>0)的轴和它的准线交于E点,经过交点F的直线交抛物线于P、Q两点(直线PQ与抛物线的轴不垂直),则∠FEP与∠QEF的大小关系为( )
| A、∠FEP>∠QEF |
| B、∠FEP<∠QEF |
| C、∠FEP=∠QEF |
| D、不确定 |
在正方体ABCD-A1B1C1D1中,BD1与AC所成的角是( )
| A、60° | B、30° |
| C、90° | D、45° |
 在正方体ABCD-A1B1C1D1中,E、F分别为棱D1C1、B1C1的中点,求平面EFC与底面ABCD所成锐二面角的正切值.
在正方体ABCD-A1B1C1D1中,E、F分别为棱D1C1、B1C1的中点,求平面EFC与底面ABCD所成锐二面角的正切值. 椭圆
椭圆