题目内容
求函数y=3sin(2x+
),x∈[0,π]的单调递减区间.
| π |
| 4 |
考点:复合函数的单调性
专题:三角函数的图像与性质
分析:根据三角函数的单调性即可得到结论.
解答:
解:由2kπ+
≤2x+
≤2kπ+
,k∈Z,
解得kπ+
≤x≤kπ+
,
当k=0时,
≤x≤
,
故此时函数的单调递减为[
,
]
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
解得kπ+
| π |
| 8 |
| 5π |
| 8 |
当k=0时,
| π |
| 8 |
| 5π |
| 8 |
故此时函数的单调递减为[
| π |
| 8 |
| 5π |
| 8 |
点评:本题主要考查三角函数单调性和单调区间的求解,根据正弦函数的单调性是解决本题的关键.

练习册系列答案
相关题目
下列函数中为偶函数的是( )
| A、y=2x |
| B、y=x2,x∈(-4,4] |
| C、y=x3 |
| D、y=x0 |
已知全集U=(-1,1),集合A={1,2},B={2,3,4},则(∁UA)∩B=( )
| A、{2} |
| B、{3,4} |
| C、{1,4,5} |
| D、{2,3,4,5} |
已知复数z1=-
+
i,z2=-
-
i,则下列命题中错误的是( )
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| A、z12=z2 |
| B、|z1|=|z2| |
| C、z13-z23=1 |
| D、zl、z2互为共轭复数 |
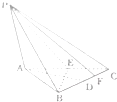 在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.
在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.