题目内容
12．
如图茎叶图记录了甲、乙两组各四名同学的植树棵树，分别从甲、乙两组中随机选取一名同学，则这两名同学的植树总棵树为20棵的概率是$\frac{1}{4}$．
分析 记甲组四名同学为a，b，c，d，乙组四名同学为E，F，G，H，写出他们植树的棵树，用列举法求出基本事件数，计算对应的概率值即可．
解答 解：记甲组四名同学为a，b，c，d，他们植树的棵树依次为9，9，11，11：
乙组四名同学为E，F，G，H，他们植树的棵树依次为9，8，9，10，
分别从甲，乙两组中随机选取一名同学，所有可能的结果有16个，它们是
（a，E）（a，F）（a，G）（a，H）（b，E）（b，F）（b，G）（b，H）
（c，E）（c，F）（c，G）（c，H）（d，E）（d，F）（d，G）（d，H）．
设选出的两名同学的植树总棵数为20为事件C，则C中的结果有4个，
它们是（c，E）（d，E）（c，G）（d，G），
故所求概率为P（C）=$\frac{1}{4}$．
点评 本题考查了用列举法求古典概型的概率问题，是基础题目．
练习册系列答案
相关题目
3．若复数z满足zi=1-i，则z的共轭复数是（ ）
| A． | -1-i | B． | 1-i | C． | -1+i | D． | 1+i |
20．
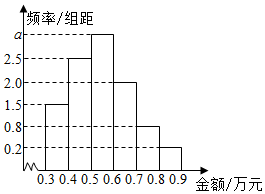某电子商务公司对10000名网络购物者2015年度的消费情况进行统计，发现消费金额（单位：万元）都在区间[0.3，0.9]，其频率分布直方图如图所示，在这些购物者中，消费金额在区间[0.5，0.9]内的购物者的人数为（ ）
某电子商务公司对10000名网络购物者2015年度的消费情况进行统计，发现消费金额（单位：万元）都在区间[0.3，0.9]，其频率分布直方图如图所示，在这些购物者中，消费金额在区间[0.5，0.9]内的购物者的人数为（ ）| A． | 3000 | B． | 4000 | C． | 5000 | D． | 6000 |
7．已知p：?m∈R，x2-mx-1=0有解，q：?x0∈N，${x_0}^2-2{x_0}-1≤0$；则下列选项中是假命题的为（ ）
| A． | p∧q | B． | p∧（￢q） | C． | p∨q | D． | p∨（￢q） |
17．已知函数f（x）=a|x|-3a-1，若命题?x0∈[-1，1]，使f（x0）=0是真命题，则实数a的取值范围为（ ）
| A． | （-∞，-$\frac{1}{2}$] | B． | （-∞，-$\frac{1}{2}$]∪（0，+∞） | C． | [-$\frac{1}{2}$，-$\frac{1}{3}$] | D． | （-∞，-$\frac{1}{3}$）∪[-$\frac{1}{2}$，0） |
1．在复平面内，复数z对应的点的坐标为（2，-1），则|z|=（ ）
| A． | $\sqrt{5}$ | B． | 5 | C． | 3 | D． | 1 |