题目内容
2.已知集合{x,xy,lg(xy)}={0,|x|,y},则log8(x2+3y2)=$\frac{2}{3}$.分析 集合和集合相等,集合中的元素都相等.
解答 解:∵集合{x,xy,lg(xy)}={0,|x|,y},
x≠0,xy≠0,故lg(xy)=0,
即xy=1,
令y=1,则x=1,不满足集合元素的互异性,
故y≠1,
则|x|=1,则x=-1,或x=1(舍去),
则y=-1,
故log8(x2+3y2)=$\frac{2}{3}$
点评 本题考查的知识点是对数的运算性质,集合相等,其中根据集合相等的定义及对数的运算性质,结合集合元素的互异性,求出a,b的值,是解答的关键

练习册系列答案
相关题目
11.函数y=$\frac{{x}^{2}-1}{\sqrt{2-|x|}}$的定义域是( )
| A. | [-2,2] | B. | (-∞,-2]∪[2,+∞) | C. | (-2,2) | D. | (-∞,-2)∪(2,+∞) |
12.设集合A={a,a2,-2},B={2,4},A∩B={4},则a=( )
| A. | 2 | B. | -2 | C. | 4 | D. | $\sqrt{2}$ |
 如图茎叶图记录了甲、乙两组各四名同学的植树棵树,分别从甲、乙两组中随机选取一名同学,则这两名同学的植树总棵树为20棵的概率是$\frac{1}{4}$.
如图茎叶图记录了甲、乙两组各四名同学的植树棵树,分别从甲、乙两组中随机选取一名同学,则这两名同学的植树总棵树为20棵的概率是$\frac{1}{4}$.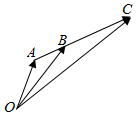 已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)
已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)