题目内容
17.已知函数f(x)=a|x|-3a-1,若命题?x0∈[-1,1],使f(x0)=0是真命题,则实数a的取值范围为( )| A. | (-∞,-$\frac{1}{2}$] | B. | (-∞,-$\frac{1}{2}$]∪(0,+∞) | C. | [-$\frac{1}{2}$,-$\frac{1}{3}$] | D. | (-∞,-$\frac{1}{3}$)∪[-$\frac{1}{2}$,0) |
分析 由于函数f(x)是偶函数,因此只考虑函数f(x)=ax-3a-1,若命题?x0∈[0,1],使f(x0)=0是真命题,即可得出.可得f(0)f(1)≤0,解出即可得出.
解答 解:由于函数f(x)是偶函数,因此只考虑函数f(x)=ax-3a-1,若命题?x0∈[0,1],使f(x0)=0是真命题,即可得出.
∴f(0)f(1)≤0,
∴(-3a-1)(-2a-1)≤0,
解得$-\frac{1}{2}≤a≤-\frac{1}{3}$,
故选:C.
点评 本题考查了不等式的解法、函数的性质、简易逻辑的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
5.在复平面内,复数g(x)满足$z({1+i})=|{1+\sqrt{3}i}|$,则z的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.已知随机变量X~N(1,σ2),若P(0<X<2)=0.4,则P(X≤0)=( )
| A. | 0.6 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
9.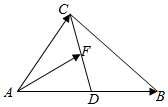 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )| A. | $6+2\sqrt{2}$ | B. | $6\sqrt{3}$ | C. | 6+4$\sqrt{2}$ | D. | $3+2\sqrt{2}$ |
 如图茎叶图记录了甲、乙两组各四名同学的植树棵树,分别从甲、乙两组中随机选取一名同学,则这两名同学的植树总棵树为20棵的概率是$\frac{1}{4}$.
如图茎叶图记录了甲、乙两组各四名同学的植树棵树,分别从甲、乙两组中随机选取一名同学,则这两名同学的植树总棵树为20棵的概率是$\frac{1}{4}$.