题目内容
13．在△ABC中，角A，B，C所对的边分别为a，b，c，且accosB-bccosA=3b2．（1）求$\frac{a}{b}$的值；
（2）若角C为锐角，c=$\sqrt{11}$，sinC=$\frac{2\sqrt{2}}{3}$，求△ABC的面积．
分析 （1）由accosB-bccosA=3b2，利用余弦定理可得$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}$-$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2}$=3b2，化简即可得出．
（2）由角C为锐角，sinC=$\frac{2\sqrt{2}}{3}$，可得cosC=$\sqrt{1-si{n}^{2}C}$．利用余弦定理可得$（\sqrt{11}）^{2}$=a2+b2-2ab×$\frac{1}{3}$，与a=2b联立解得b，a，即可得出．
解答 解：（1）∵accosB-bccosA=3b2，
∴$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}$-$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2}$=3b2，化为：a=2b，因此$\frac{a}{b}$=2．
（2）∵角C为锐角，sinC=$\frac{2\sqrt{2}}{3}$，∴cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{1}{3}$．
∴$（\sqrt{11}）^{2}$=a2+b2-2ab×$\frac{1}{3}$，化为：3a2+3b2-2ab=33，又a=2b，
联立解得b2=3，∴S△ABC=$\frac{1}{2}ab$sinC=$\frac{1}{2}×2{b}^{2}sinC$=$3×\frac{2\sqrt{2}}{3}$=2$\sqrt{2}$．
点评 本题考查了余弦定理、同角三角函数基本关系式、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
4．已知角θ的终边过点（2sin2$\frac{π}{8}$-1，a），若sinθ=2$\sqrt{3}$sin$\frac{13π}{12}$cos$\frac{π}{12}$，则实数a等于（ ）
| A． | -$\sqrt{6}$ | B． | -$\frac{\sqrt{6}}{2}$ | C． | ±$\sqrt{6}$ | D． | ±$\frac{\sqrt{6}}{2}$ |
1．
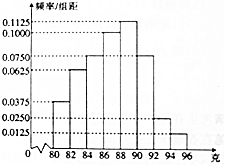某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）
某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）| A． | 第3组 | B． | 第4组 | C． | 第5组 | D． | 第6组 |
8．已知抛物线C：y2=2px（p＞0）的焦点为F，点M（x0，2$\sqrt{2}$）是抛物线C上一点，圆M与y轴相切且与线段MF相交于点A，若$\frac{|MA|}{|AF|}$=2，则p等于（ ）
| A． | 1 | B． | 2 | C． | 2$\sqrt{2}$ | D． | 4 |
2．已知x，y满足$\left\{\begin{array}{l}{y≥x}&{\;}\\{x+y≤2}&{\;}\\{x≥a}&{\;}\end{array}\right.$，且z=2x-y的最大值是最小值的-2倍，则a=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |