题目内容
8.已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0,2$\sqrt{2}$)是抛物线C上一点,圆M与y轴相切且与线段MF相交于点A,若$\frac{|MA|}{|AF|}$=2,则p等于( )| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 设M到准线的距离为|MB|,则|MB|=|MF|,利用$\frac{|MA|}{|AF|}$=2,得x0=p,即可得出结论.
解答 解:设M到准线的距离为|MB|,则|MB|=|MF|,
∵$\frac{|MA|}{|AF|}$=2,∴x0=p,
∴2p2=8,
∵p>0,
∴p=2.
故选B.
点评 本题考查抛物线定义的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
3.已知函数f(x)=-x2-6x-3,g(x)=2x3+3x2-12x+9,m<-2,若?x1∈[m,-2),?x2∈(0,+∞),使得f(x1)=g(x2)成立,则m的最小值为( )
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
20.设集合A={x∈R|x-1>0},B={x∈R|x<0},C={x∈R|x(x-2)>0},则“x∈A∪B“是“x∈C“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.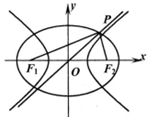 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )| A. | e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | B. | e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | ||
| C. | e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ | D. | e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ |
18.《九章算术》有这样一个问题:今有女子善织,日增等尺,第二日、第五日、第八日所织之和为十五尺,九日共织尺数是( )
| A. | 5 | B. | 15 | C. | 45 | D. | 10 |
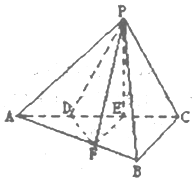 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.