题目内容
2.已知x,y满足$\left\{\begin{array}{l}{y≥x}&{\;}\\{x+y≤2}&{\;}\\{x≥a}&{\;}\end{array}\right.$,且z=2x-y的最大值是最小值的-2倍,则a=( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得到z的最值,再由z=2x+y的最大值是最小值的2倍列式求得a值.
解答 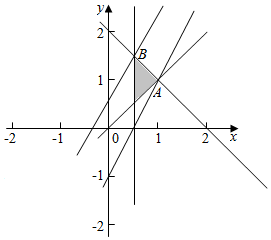 解:由约束条件$\left\{\begin{array}{l}{y≥x}&{\;}\\{x+y≤2}&{\;}\\{x≥a}&{\;}\end{array}\right.$,作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{y≥x}&{\;}\\{x+y≤2}&{\;}\\{x≥a}&{\;}\end{array}\right.$,作出可行域如图,
联立$\left\{\begin{array}{l}{x=a}\\{x+y=2}\end{array}\right.$,得B(a,2-a),
联立$\left\{\begin{array}{l}{y=x}\\{x+y=2}\end{array}\right.$,得A(1,1),
化目标函数z=2x-y为y=2x-z,
由图可知zmax=2×1-1=1,zmin=2a-2+a=3a-2,
由$\frac{1}{3a-2}$=-2,解得:a=$\frac{1}{2}$.
故选:A.
点评 本题考查了简单的线性规划考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
12.当x>0时,函数f(x)=(aex+b)(x-2)单调递增,且函数y=f(x-1)的图象关于直线x=1对称,则使得f(2-m)>0成立的m的取值范围是( )
| A. | {m|m<-2或m>2} | B. | {m|-2<m<2} | C. | {m|m<0或m>4} | D. | {m|0<m<4} |
17.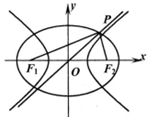 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )| A. | e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | B. | e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | ||
| C. | e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ | D. | e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ |
12.已知a=20.1,$b={({\frac{1}{2}})^{-0.4}}$,c=2log72,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | b<c<a |