题目内容
18.设实数x,y满足x+$\frac{y}{4}$=1.(1)若|7-y|<2x+3,求x的取值范围;
(2)若x>0,y>0,求证:$\sqrt{xy}$≥xy.
分析 (1)根据题意,由x+$\frac{y}{4}$=1,则y=4-4x,则|7-y|<2x+3,可得|4x+3|<2x+3,解可得x的范围,即可得答案;
(2)根据题意,由基本不等式可得1=x+$\frac{y}{4}$≥2$\sqrt{x•\frac{y}{4}}$=$\sqrt{xy}$,即$\sqrt{xy}$≤1,用作差法分析可得$\sqrt{xy}$-xy=$\sqrt{xy}$(1-$\sqrt{xy}$),结合$\sqrt{xy}$的范围,可得$\sqrt{xy}$-xy≥0,即可得证明.
解答 解:(1)根据题意,若x+$\frac{y}{4}$=1,则4x+y=4,即y=4-4x,
则由|7-y|<2x+3,可得|4x+3|<2x+3,
即-(2x+3)<4x+3<2x+3,
解可得-1<x<0;
(2)证明:x>0,y>0,1=x+$\frac{y}{4}$≥2$\sqrt{x•\frac{y}{4}}$=$\sqrt{xy}$,即$\sqrt{xy}$≤1,
$\sqrt{xy}$-xy=$\sqrt{xy}$(1-$\sqrt{xy}$),
又由0<$\sqrt{xy}$≤1,则$\sqrt{xy}$-xy=$\sqrt{xy}$(1-$\sqrt{xy}$)≥0,
即$\sqrt{xy}$≥xy.
点评 本题考查基本不等式、绝对值不等式的应用,关键是利用x+$\frac{y}{4}$=1分析变量x、y之间的关系.

练习册系列答案
相关题目
9.下列选项中,说法正确的是( )
| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| C. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
6.已知集合A={x|(x-2)(x+6)>0},B={x|-3<x<4},则A∩B等于( )
| A. | (-3,-2) | B. | (-3,2) | C. | (2,4) | D. | (-2,4) |
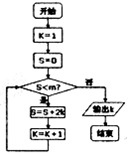
3.执行如图所示的程序框图,若输出的结果是6,则判断框内m的取值范围是( )

| A. | (30,42] | B. | (20,30) | C. | (20,30] | D. | (20,42) |
8.定义域为R的偶函数f(x)满足?x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(x+1)恰有三个零点,则a的取值范围是( )
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | (0,$\frac{\sqrt{3}}{3}$) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{6}}{6}$,$\frac{\sqrt{5}}{5}$) |