题目内容
1．
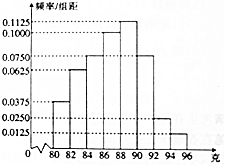某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）| A． | 第3组 | B． | 第4组 | C． | 第5组 | D． | 第6组 |
分析 根据频率分布直方图求出前4组的频数为22，且第四组的频数8，即可得到答案．
解答 解：由图可得，前第四组的频率为（0.0375+0.0625+0.075+0.1）×2=0.55，
则其频数为40×0.55=22，且第四组的频数为40×0.1×2=8，
故中位数落在第4组，
故选：B
点评 本题是对频率、频数灵活运用的综合考查．频率、频数的关系：频率=频数÷数据总和，以及中位数的定义，属于基础题．
练习册系列答案
相关题目
11．设集合M={x|x2+3x+2＞0}，集合N={-2，-1，0，1，2}，则M∩N=（ ）
| A． | {-2，-1} | B． | {0，1，2} | C． | {-1，0，1，2} | D． | {-2，-1，0，1，2} |
12．当x＞0时，函数f（x）=（aex+b）（x-2）单调递增，且函数y=f（x-1）的图象关于直线x=1对称，则使得f（2-m）＞0成立的m的取值范围是（ ）
| A． | {m|m＜-2或m＞2} | B． | {m|-2＜m＜2} | C． | {m|m＜0或m＞4} | D． | {m|0＜m＜4} |
9．下列选项中，说法正确的是（ ）
| A． | 命题“?x0∈R，x02-x0≤0”的否定为“?x∈R，x2-x＞0” | |
| B． | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|，则$\overrightarrow a$与$\overrightarrow b$共线 | |
| C． | 命题“在△ABC中，A＞30°，则sinA＞$\frac{1}{2}$”的逆否命题为真命题 | |
| D． | 设{an}是公比为q的等比数列，则“q＞1”是“{an}为递增数列”的充分必要条件 |
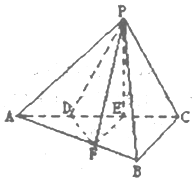如图，三棱锥P-ABC中，平面PAC⊥平面ABC，∠ABC=$\frac{π}{2}$，点D、E在线段AC上，且AD=DE=EC=1，PD=PC=2，点F在线段AB上，且EF∥BC．
6．已知集合A={x|（x-2）（x+6）＞0}，B={x|-3＜x＜4}，则A∩B等于（ ）
| A． | （-3，-2） | B． | （-3，2） | C． | （2，4） | D． | （-2，4） |