题目内容

13．已知$f（{2^x}）=\frac{1}{x}$，则f（3）=（　　）
A．$\frac{1}{3}$B．$\frac{1}{8}$C．log32D．log23

分析 设2x=t，则x=log2t．从而f（t）=$\frac{1}{lo{g}_{2}t}$，由此能求出f（3）．

解答 解：∵$f（{2^x}）=\frac{1}{x}$，
设2x=t，则x=log2t．
∴f（t）=$\frac{1}{lo{g}_{2}t}$，
∴f（3）=$\frac{1}{lo{g}_{2}3}$=log32．
故选：C．

点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

练习册系列答案
相关题目
3．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=2-t}\end{array}\right.$（t为参数）；以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=4$\sqrt{2}$sin（θ+$\frac{π}{4}$），直线l与曲线C的交于A，B两点．
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）求|AB|的值．
4．已知f（x+1）=f（x-1），f（x）=f（2-x），方程f（x）=0在[0，1]内只有一个根x=$\frac{1}{2}$，则f（x）=0在区间[0，2016]内根的个数2016．
1．已知数列{an}满足a1=1，an+1=2an+3，n∈N*．
（Ⅰ）求证：数列{an+3}是等比数列；
（Ⅱ）求数列{nan}的前n项和Sn．
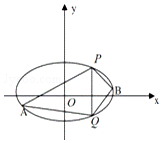8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，椭圆C的一个短轴端点与抛物线x2=4y的焦点重合．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆C右焦点的直线l交椭圆于A，B两点，若以AB为直径的圆过原点，求直线l方程．
18．设函数f（x）=$\frac{1-a}{2}$x2+ax-lnx，a∈R，
（Ⅰ）当a=1时，求函数f（x）的极值；
（Ⅱ）当a＞1时，讨论函数f（x）的单调性；
（Ⅲ）若对任意a∈（3，4）及任意x1，x2∈[1，2]，恒有$\frac{{（{a^2}-1）}}{2}m+ln2＞|{f（{x_1}）-f（{x_2}）}$|成立，求实数m的取值范围．
5．设函数f（x）=|x-1|-2|x+1|的最大值为m
（I）求m的值；
（ II）若a，b，c∈（0，+∞）），且a2+3b2+2c2=m，求ab+2bc的最大值．
2．若集合M={x∈Z||x|≤2}，N={x|x2+2x-3＜0}，则M∩N=（　　）
A．[-2，1）B．[-2，1]C．{-2，-1，0}D．{-1，0}
3．已知如下等式：2+4=6；8+10+12=14+16；18+20+22+24=26+28+30；…以此类推，则2018会出现在第（　　）个等式中．
A．33B．30C．31D．32

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网