题目内容
已知双曲线C1:
-y2=1的左,右焦点分别为F1,F2,椭圆C2:
+y2=1,点P为C1与C2的一个交点,则△PF1F2的面积为( )
| x2 |
| 3 |
| x2 |
| 5 |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意可得,F1,F2是双曲线C1与椭圆C2的共同焦点,从而利用圆锥曲线的定义去解.
解答:
解:由题意可得,
F1,F2是双曲线C1与椭圆C2的共同焦点,
故|PF1|+|PF2|=2
,
||PF1|-PF2||=2
,
|F1F2|=4,
则|PF1|2+|PF2|2
=
[(|PF1|+|PF2|)2+(|PF1|-|PF2|)2]
=
×(20+12)=16,
则△PF1F2为直角三角形,
又∵|PF1|•|PF2|
=
[(|PF1|+|PF2|)2-(|PF1|-|PF2|)2]
=
×(20-12)=2,
故S=
×|PF1|•|PF2|=1.
故选B.
F1,F2是双曲线C1与椭圆C2的共同焦点,
故|PF1|+|PF2|=2
| 5 |
||PF1|-PF2||=2
| 3 |
|F1F2|=4,
则|PF1|2+|PF2|2
=
| 1 |
| 2 |
=
| 1 |
| 2 |
则△PF1F2为直角三角形,
又∵|PF1|•|PF2|
=
| 1 |
| 4 |
=
| 1 |
| 4 |
故S=
| 1 |
| 2 |
故选B.
点评:本题考查了圆锥曲线的定义的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若“0≤x≤4”是“(x-a)[x-(a+2)]≤0”的必要不充分条件,则实数a的取值范围是( )
| A、(0,2) |
| B、[0,2] |
| C、[-2,0] |
| D、(-2,0) |
设集合A={x|x2-x=0},B={x|x2+x=0},则集合A∪B=( )
| A、0 | B、{0} |
| C、∅ | D、{-1,0,1} |
设动点A、B均在双曲线C:
-
=1(a>0,b>0)的右支上,点O为坐标原点,双曲线C的离心率为e,则( )
| x2 |
| a2 |
| y2 |
| b2 |
A、若e>
| ||||||
B、若1≤e≤
| ||||||
C、若e>
| ||||||
D、若1<e≤
|
已知|F1F2|=m,点P到两点F1、F2距离之差的绝对值为n(n<m).设点P的轨迹为C,过F1作AB⊥F1F2且交曲线C于点A、B,若△ABF2是直角三角形,则
的值为( )
| m |
| n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
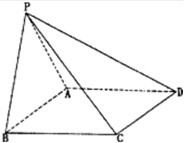 如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.
如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.