题目内容
17.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,则$\overrightarrow{a}$•$\overrightarrow{b}$=-3.分析 根据条件及数量积的计算公式即可求出数量积$\overrightarrow{a}•\overrightarrow{b}$的值.
解答 解:根据条件:
$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°$=$2×3×(-\frac{1}{2})=-3$.
故答案为:-3.
点评 考查向量长度及夹角的定义,以及向量数量积的计算公式.

练习册系列答案
相关题目
5.函数f(x)=2x+x-2的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
6.下列求导运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | ||
| C. | (3x)′=3x•log 3e | D. | (x2cos x)′=-2xsin x |
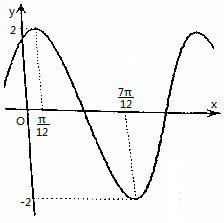 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.