题目内容
8.设x>0,当x=4时,x+$\frac{16}{x}$有最小值,最小值为8.分析 利用基本不等式的性质即可得出.
解答 解:∵x>0,∴x+$\frac{16}{x}$≥$2\sqrt{x•\frac{16}{x}}$=8,当且仅当x=4时取等号,
因此当x=4时,x+$\frac{16}{x}$有最小值8,
故答案为:4,8.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
3.某几何体三视图如图所示,则该几何体的最短的棱长度是( )
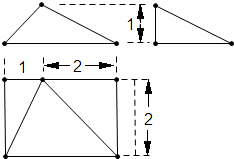

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
20.函数f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$ax2-2ax+2a+1的图象经过四个象限的一个充分但不必要条件是( )
| A. | -$\frac{4}{3}$<a<-$\frac{1}{3}$ | B. | -1<a<-$\frac{1}{2}$ | C. | -$\frac{6}{5}$<a<-$\frac{3}{16}$ | D. | -2<a<0 |