题目内容

17．已知f（x）=（x-m）（x-n）（其中n＜m）的图象如图所示，则函数g（x）=mx+n的图象大致是（　　）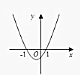
A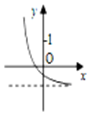．B．C．D．

分析 根据f（x）的图象可得n＜-1，0＜m＜1，再根据指数函数的图象即可判断．

解答 解：由f（x）=（x-m）（x-n）的图象可知，n＜-1，0＜m＜1，
∴g（x）=mx+n在R上为减函数，当x=0时，g（0）=1+n＜0，
故选：A．

点评 本题考查了函数图象的识别和指数函数和二次函数的图象的性质，属于基础题．

练习册系列答案
相关题目
7．根据表格中的数据用最小二乘法计算出变量x、y的线性回归方程为$\stackrel{∧}{y}$=3x-$\frac{3}{2}$，则表格中m的值是（　　）
x0123
y-118m
A．4B．$\frac{9}{2}$C．5D．6
8．设x＞0，当x=4时，x+$\frac{16}{x}$有最小值，最小值为8．
5．已知集合A={x|-1＜x＜3}，B={x|0＜x＜4}，则A∪B=（　　）
A．（-1，4）B．（-1，0）C．（0，3）D．（3，4）
12．若M∪{1}={1，2，3}，则M集合可以是（　　）
A．{1，2，3}B．{1，3}C．{1，2}D．{1}
2．下列命题：
①函数y=-$\frac{1}{x}$在其定义域上是增函数；
②函数y=$\frac{x（x+1）}{x+1}$是奇函数；
③函数y=log2（x-1）的图象可由y=log2（x+1）的图象向右平移2个单位得到；
④若（$\frac{1}{2}$）a=（$\frac{1}{3}$）b＜1．则a＜b＜0
则下列正确命题的序号是③．
9．以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据
房屋面积（平方米）11511080135105
销售价格（万元）24.821.618.429.222
（1）画出散点图
（2）求线性回归方程
（3）根据（2）的结果估计房屋面积为150平方米时的销售价格．
17．某大型商场成立十周年之际，为了回馈顾客，特进行有奖销售：有奖销售期间，每购买满100元该商场的商品，都有一次抽奖机会，一旦中奖，将获得相应的奖品；抽奖方案是：从装有3个红色小球A、B、C和3个白色小球f'（x0）=0的箱子里摸出2个小球，若2个都是红球就中一等奖、恰有1个是红球就中二等奖，否则无奖；其中箱子里的小球除颜色和编号外完全相同．
（Ⅰ）若某顾客抽奖一次，求他获得一等奖的概率．
（Ⅱ）若某顾客抽奖一次，求他获奖的概率．
18．已知a，b为正实数，a+b=1，且a，b的值使$\frac{1}{a}+\frac{4}{b}$取得最小值，此最小值为m，则函数f（x）=ax3-4x2-mx+1的极大值为（　　）
A．4B．$\frac{25}{3}$C．-89D．$\frac{17}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网