题目内容
18.已知高与底面半径相等的圆锥的体积为$\frac{8π}{3}$,其侧面积与球O的表面积相等,则球O的表面积为4$\sqrt{2}$π.分析 利用高与底面半径相等的圆锥的体积为$\frac{8π}{3}$,求出底面半径,利用其侧面积与球O的表面积相等,即可求出球O的表面积.
解答 解:由题意,设底面半径为r,
则圆锥的体积为$\frac{1}{3}π•{r}^{2}•r$=$\frac{8π}{3}$,
∴r=2,
∴侧面积=$π•2•2\sqrt{2}$=4$\sqrt{2}$π
∴球O的表面积=4$\sqrt{2}$π.
故答案为4$\sqrt{2}$π.
点评 本题考查圆锥的体积,球O的表面积,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.函数f(x)=4sin($\frac{1}{2}$x+$\frac{π}{6}$)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
13.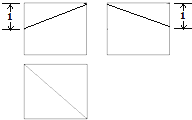 一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
 一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )| A. | $\frac{22}{3}$ | B. | $\frac{20}{3}$ | C. | 6 | D. | 4 |
3.已知函数f(x)=2ax3-3ax2+1,g(x)=-$\frac{a}{4}x+\frac{3}{2}$,若对任意给定的m∈[0,2],关于x的方程f(x)=g(m)在区间[0,2]上总存在两个不同的解,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | [-1,1] |
10.在数列{an}中,a1=-$\frac{1}{4}$,an=1-$\frac{1}{{a}_{n-1}}$(n>1),则a2016的值为( )
| A. | -$\frac{1}{4}$ | B. | 5 | C. | $\frac{4}{5}$ | D. | 以上都不对 |
7.根据表格中的数据用最小二乘法计算出变量x、y的线性回归方程为$\stackrel{∧}{y}$=3x-$\frac{3}{2}$,则表格中m的值是( )
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | 8 | m |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |