题目内容
13．如图所示的四个函数图象，在区间（-∞，0）内，方程fi（x）=0（i=1，2，3，4）有实数解的是（ ）| A． |  | B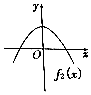． |  | C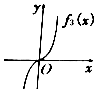． |  | D． |  |
分析 若在区间（-∞，0）内，方程fi（x）=0（i=1，2，3，4）有实数解，则函数图象与x轴负半轴有交点，进而得到答案．
解答 解：若在区间（-∞，0）内，方程fi（x）=0（i=1，2，3，4）有实数解，
则函数图象与x轴负半轴有交点，
故选：B
点评 本题考查的知识点是函数的图象，方程的根与函数零点的关系，难度中档．
练习册系列答案
相关题目
3．已知函数f（x）=2ax3-3ax2+1，g（x）=-$\frac{a}{4}x+\frac{3}{2}$，若对任意给定的m∈[0，2]，关于x的方程f（x）=g（m）在区间[0，2]上总存在两个不同的解，则实数a的取值范围是（ ）
| A． | （-∞，-1） | B． | （1，+∞） | C． | （-∞，-1）∪（1，+∞） | D． | [-1，1] |
4．
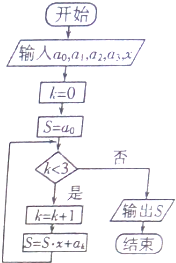如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法，执行该程序框图，则输出的结果S表示的值为（ ）
如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法，执行该程序框图，则输出的结果S表示的值为（ ）| A． | a0+a1+a2+a3 | B． | （a0+a1+a2+a3）x3 | ||
| C． | a0+a1x+a2x2+a3x3 | D． | a0x3+a1x2+a2x+a3 |
5．已知集合A={x|-1＜x＜3}，B={x|0＜x＜4}，则A∪B=（ ）
| A． | （-1，4） | B． | （-1，0） | C． | （0，3） | D． | （3，4） |