题目内容
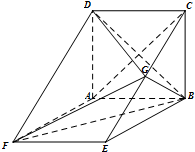 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.(1)求证:AC∥平面BFG;
(2)若三棱锥C-DGB的体积为
| 9 |
| 4 |
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)根据线线平行得到线面平行即可,(2)先求出三角形BCE的面积,从而求出三棱柱ADF-BCE的体积.
解答:
解:(1)如图示:

连结AE交BF于点O,连结OG,
∵O、G分别是AE、CE的中点,
∴OG∥AC,
∵AC?平面BFG,OG?平面BFG,
∴AC∥平面BFG;
(2)∵VC-DGB=
•S△BCG•3=
,
∴S△BCG=
,
∴S△BCE=
,
∴三棱柱ADF-BCE的体积是:3×
=
.

连结AE交BF于点O,连结OG,
∵O、G分别是AE、CE的中点,
∴OG∥AC,
∵AC?平面BFG,OG?平面BFG,
∴AC∥平面BFG;
(2)∵VC-DGB=
| 1 |
| 3 |
| 9 |
| 4 |
∴S△BCG=
| 9 |
| 4 |
∴S△BCE=
| 9 |
| 2 |
∴三棱柱ADF-BCE的体积是:3×
| 9 |
| 2 |
| 27 |
| 2 |
点评:本题考查了面面平行的判定定理,考查了求几何体的体积问题,本题属于中档题.

练习册系列答案
相关题目
若a=20.5,b=ln2,c=0.5e(e是自然对数的底),则( )
| A、a<b<c |
| B、b>a>c |
| C、a>c>b |
| D、a>b>c |
已知i是虚数单位,m和n都是实数,且m(1+i)=
+ni,则(
)2015=( )
| 3 |
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
从地面上测一建在山顶上的建筑物,测得其视角为α,同时测得建筑物顶部仰角为β,则山顶的仰角为( )
| A、α+β | B、α-β |
| C、β-α | D、α |