题目内容

求导：y=sin（cosx2）
考点：导数的运算
专题：导数的概念及应用
分析：根据函数的导数公式进行求导即可．
解答： 解：函数的导数为y′=cos（cosx2）（cosx2）′=cos（cosx2）（-sinx2）（2x）′
=-2cos（cosx2）（-sinx2）．
点评：本题主要考查函数的导数的求解，根据复合函数的导数公式是解决本题的关键．
练习册系列答案
相关题目
已知x＞0，则（x+
1
x
+2）3的展开式中常数项是
 
．
函数f（x）=sinx+cosx的单调增区间为
 
，已知sinα=
3
5
，且α∈（0，
π
2
），则f（α-
π
12
）=
 
．
在利用电子邮件传播病毒的例子中，如果第一轮感染的计算机数是80台，并且从第一轮起，以后各轮的每一台计算机都可以感染下一轮的20台计算机，第5轮可以感染到多少台计算机？
化简：
sin(3π+α)cos(π-α)tan(π-α)cos(-α)
sin(5π-α)cos(3π+α)sin(-α)
．
“?p为假命题”是“p∧q为真命题”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
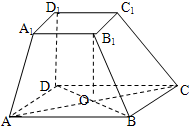如图，在四棱台ABCD-A1B1C1D1中，DD1⊥平面ABCD，底面ABCD是平行四边形，AB=AD=2A1B1，∠BAD=60°
（1）证明：BB1⊥AC；
（2）若AB=2，且二面角A1-AB-C大小为60°，连接AC，BD，设交点为O，连接B1O．求三棱锥B1-ABO外接球的体积．
（球体体积公式：V=
4
3
πR3，R是球半径）
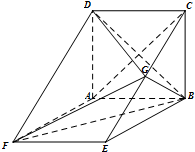如图，ABCD是边长为3的正方形，ABEF是矩形，平面ABCD⊥平面ABEF，G为EC的中点．
（1）求证：AC∥平面BFG；
（2）若三棱锥C-DGB的体积为
9
4
，求三棱柱ADF-BCE的体积．
已知x+y=-1，且x，y都是负实数，则xy+
1
xy
有（　　）
A、最小值2
B、最大值-2
C、最小值
17
4
D、最大值-
17
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网