题目内容
若a=20.5,b=ln2,c=0.5e(e是自然对数的底),则( )
| A、a<b<c |
| B、b>a>c |
| C、a>c>b |
| D、a>b>c |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用指数函数与对数函数的单调性即可得出.
解答:
解:∵a=20.5>1,1>b=ln2>ln
=
,c=0.5e<0.51=
.
∴a>b>c.
故选:D.
| e |
| 1 |
| 2 |
| 1 |
| 2 |
∴a>b>c.
故选:D.
点评:本题考查了指数函数与对数函数的单调性,考查了推理能力,属于基础题.

练习册系列答案
相关题目
“?p为假命题”是“p∧q为真命题”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数 f(x)=
cos2x+
sinxcosx的一个对称中心是( )
| 1 |
| 2 |
| 3 |
A、(
| ||
B、(
| ||
C、(-
| ||
D、(-
|
若变量x、y满足条件
,则z=2x-y的取值范围是( )
|
| A、[-2,4] |
| B、(-2,4] |
| C、[-2,4) |
| D、(-2,4) |
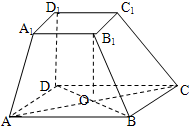 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°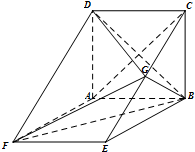 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.