题目内容

9．已知函数y=f（x+2）的定义域为（0，2），则函数y=$\frac{f（x）}{x-2}$的定义域为（2，4）．

分析 由已知函数定义域求得y=f（x）的定义域，再结合分母不为0得答案．

解答 解：∵y=f（x+2）的定义域为（0，2），即0＜x＜2，
∴2＜x+2＜4，即y=f（x）的定义域为（2，4），
由$\left\{\begin{array}{l}{2＜x＜4}\\{x-2≠0}\end{array}\right.$，得2＜x＜4．
∴函数y=$\frac{f（x）}{x-2}$的定义域为（2，4）．
故答案为：（2，4）．

点评 本题考查函数的定义域及其求法，关键是掌握该类问题的求解方法，是中档题．

练习册系列答案
相关题目
19．（1）设复数z满足|z|=5，且（3+4i）z是纯虚数，求z．
（2）已知m＞0，a，b∈R，求证：（$\frac{a+mb}{1+m}$）2≤$\frac{{a}^{2}+m{b}^{2}}{1+m}$．
20．如图是一个面积为1的三角形，现进行如下操作．第一次操作：分别连结这个三角形三边的中点，构成4个三角形，挖去中间一个三角形（如图①中阴影部分所示），并在挖去的三角形上贴上数字标签“1”；第二次操作：连结剩余的三个三角形三边的中点，再挖去各自中间的三角形（如图②中阴影部分所示），同时在挖去的3个三角形上都贴上数字标签“2”；第三次操作：连结剩余的各三角形三边的中点，再挖去各自中间的三角形，同时在挖去的三角形上都贴上数字标签“3”；…，如此下去．记第n次操作中挖去的三角形个数为an．如a1=1，a2=3．

（1）求an；
（2）求第n次操作后，挖去的所有三角形面积之和Pn？
（3）求第n次操作后，挖去的所有三角形上所贴标签上的数字和Qn．
17．已知M={x|y=$\sqrt{1-lo{g}_{2}x}$}，N={x|x2-2x-3＜0}，则M∩N=（　　）
A．（0，2）B．（-1，2]C．（0，2]D．（-1，3）
4．函数f（x）=$\frac{{9}^{x}-a}{{3}^{x}}$的图象关于原点对称，则a=（　　）
A．1B．-1C．-$\frac{1}{2}$D．$\frac{1}{2}$
14．计算：（0.027）${\;}^{\frac{1}{3}}$-（6$\frac{1}{4}$）${\;}^{\frac{1}{2}}$+（2$\sqrt{2}$）${\;}^{-\frac{2}{3}}$+π0-3-1=-$\frac{31}{30}$．
1．把函数g（x）=sin（x-$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$个单位可以得到函数f（x）的图象，则f（$\frac{π}{6}$）=（　　）
A．-$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．-1D．1
18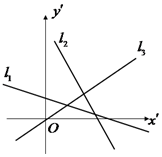．如图，在平面直角坐标系中有三条直线l1，l2，l3，其对应的斜率分别为k1，k2，k3，则下面选项中正确的是（　　）
A．k3＞k1＞k2B．k1-k2＜0C．k2•k3＞0D．k3＞k2＞k1
19．函数f（x）=$\frac{1}{\sqrt{lo{g}_{2}x-1}}$的定义域为（　　）
A．（0，2）B．[2，+∞）C．（0，2]D．（2，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网