题目内容
18.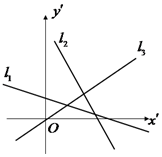 如图,在平面直角坐标系中有三条直线l1,l2,l3,其对应的斜率分别为k1,k2,k3,则下面选项中正确的是( )
如图,在平面直角坐标系中有三条直线l1,l2,l3,其对应的斜率分别为k1,k2,k3,则下面选项中正确的是( )| A. | k3>k1>k2 | B. | k1-k2<0 | C. | k2•k3>0 | D. | k3>k2>k1 |
分析 由图形可得:三条直线l1,l2,l3的倾斜角θi(i=1,2,3)满足:π>θ2>θ1>$\frac{π}{2}$>θ3>0,利用正切函数的单调性与斜率的计算公式即可得出.
解答 解:由图形可得:三条直线l1,l2,l3的倾斜角θi(i=1,2,3)满足:π>θ1>θ2>$\frac{π}{2}$>θ3>0,
∴k3>k1>k2.
故选:A.
点评 本题考查了正切函数的单调性与斜率的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.设f(x)<0是定义在R上的奇函数,且f(2)<0,当x>0时,有$\frac{xf′(x)-f(x)}{{x}^{2}}$<0恒成立,则不等式x2f(x)>0的解集是( )
| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
7.已知tanα=-3,tan(α-2β)=1,则tan4β=( )
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | 2 | D. | -2 |