题目内容
4.一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的3只球中的最大号码,写出随机变量ξ的分布列.分析 根据题意得出随机变量ξ的取值为3,4,5;计算对应的概率值,写出ξ的分布列.
解答 解:随机变量ξ的取值为3,4,5;
P(ξ=3)=$\frac{{C}_{2}^{2}}{{C}_{5}^{3}}$=$\frac{1}{10}$,
P(ξ=4)=$\frac{{C}_{3}^{2}}{{C}_{5}^{3}}$=$\frac{3}{10}$,
P(ξ=5)=$\frac{{C}_{4}^{2}}{{C}_{5}^{3}}$=$\frac{6}{10}$=$\frac{3}{5}$;
因此ξ的分布列为
| ξ | 3 | 4 | 5 |
| P | $\frac{1}{10}$ | $\frac{3}{10}$ | $\frac{6}{10}$ |
点评 本题考查了离散型随机变量的概率与分布列的计算问题,是基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
15.两封信随机地投入到编号为A,B,C的三个空邮筒中,则A邮筒中信件数x的数学期望E(x)等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
14.若f(x)=$\frac{1}{2}$ax2+2x-lnx(a≠0)在区间[1,2]上是增函数,则实数a的最小值为( )
| A. | 1 | B. | -1 | C. | -$\frac{3}{4}$ | D. | -2 |
 如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.
如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.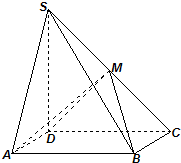 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.