题目内容
2.在△ABC中,A,B为锐角,且cos 2A=$\frac{3}{5}$,sin B=$\frac{\sqrt{10}}{10}$,求角C的大小.分析 根据同角的三角函数的关系以及两角和的余弦公式即可求出.
解答 解:在△ABC中,∵A为锐角,cos 2A=$\frac{3}{5}$,
∴cos2A=1-2sin2A=$\frac{3}{5}$,
∴sinA=$\frac{\sqrt{5}}{5}$,cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{2\sqrt{5}}{5}$.
又B为锐角,sin B=$\frac{\sqrt{10}}{10}$,
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{3\sqrt{10}}{10}$,
∴cos(A+B)=cosAcosB-sinAsinB=$\frac{2\sqrt{5}}{5}$×$\frac{3\sqrt{10}}{10}$-$\frac{\sqrt{5}}{5}$×$\frac{\sqrt{10}}{10}$=$\frac{\sqrt{2}}{2}$,
∵0<A+B<π,
∴A+B=$\frac{π}{4}$,
∴C=π-(A+B)=$\frac{3π}{4}$.
点评 本题考查了同角的三角函数的关系和两角和的余弦公式,考查了学生的运算能力,属于基础题

练习册系列答案
相关题目
16.若点P对应的复数z满足|z|≤1,则P的轨迹是( )
| A. | 直线 | B. | 线段 | C. | 圆 | D. | 单位圆以及圆内 |
12.圆x2+y2+4x-2y+$\frac{24}{5}$=0上的点到直线3x+4y=0的距离的最大值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{2+\sqrt{5}}{5}$ | D. | $\frac{2-\sqrt{5}}{5}$ |
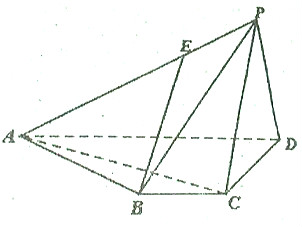 如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.