题目内容
已知圆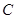 的圆心在直线
的圆心在直线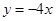 上,且与直线
上,且与直线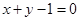 相切于点
相切于点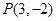 .
.
(Ⅰ)求圆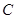 方程;
方程;
(Ⅱ)点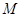
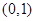 与点
与点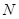 关于直线
关于直线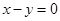 对称.是否存在过点
对称.是否存在过点 的直线
的直线 ,
, 与圆
与圆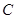 相交于
相交于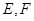 两点,且使三角形
两点,且使三角形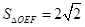 (
(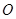 为坐标原点),若存在求出直线
为坐标原点),若存在求出直线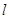 的方程,若不存在用计算过程说明理由.
的方程,若不存在用计算过程说明理由.
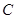 的圆心在直线
的圆心在直线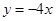 上,且与直线
上,且与直线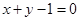 相切于点
相切于点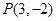 .
.(Ⅰ)求圆
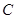 方程;
方程;(Ⅱ)点
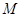
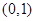 与点
与点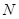 关于直线
关于直线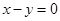 对称.是否存在过点
对称.是否存在过点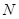 的直线
的直线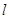 ,
,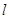 与圆
与圆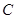 相交于
相交于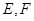 两点,且使三角形
两点,且使三角形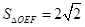 (
(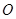 为坐标原点),若存在求出直线
为坐标原点),若存在求出直线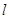 的方程,若不存在用计算过程说明理由.
的方程,若不存在用计算过程说明理由.(Ⅰ)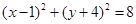 ;(Ⅱ)
;(Ⅱ)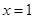
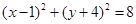 ;(Ⅱ)
;(Ⅱ)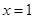
试题分析:(Ⅰ)首先求得过圆心与切点的直线,然后与直线
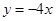 联立可求得圆心,再利用两点间的距离公式可求得半径,进而求得圆的方程;(Ⅱ)首先根据对称性求得
联立可求得圆心,再利用两点间的距离公式可求得半径,进而求得圆的方程;(Ⅱ)首先根据对称性求得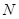 的坐标,然后分直线
的坐标,然后分直线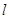 的斜率是否存在两种情况求解,求解过程中注意利用点到直线的距离公式.
的斜率是否存在两种情况求解,求解过程中注意利用点到直线的距离公式.试题解析:(Ⅰ)过切点
 且与
且与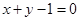 垂直的直线为
垂直的直线为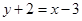 ,即
,即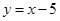 .
.与直线
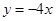 联立可求圆心为
联立可求圆心为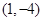 ,
, 所以半径
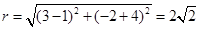 ,
,所以所求圆的方程为
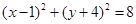 .
.(Ⅱ)设
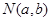 ,∵点
,∵点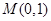 与点
与点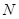 关于直线
关于直线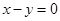 对称,
对称,∴
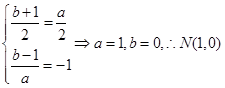 .
.注意:若没证明,直接得出结果
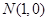 ,不扣分.
,不扣分.1.当斜率不存在时,此时直线
 方程为
方程为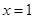 ,原点到直线的距离为
,原点到直线的距离为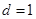 ,
,同时令
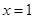 代人圆方程得
代人圆方程得 ,∴
,∴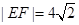 ,
,∴
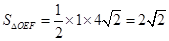 满足题意,此时方程为
满足题意,此时方程为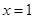 .
.2.当斜率存在时,设直线
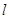 的方程为
的方程为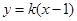 ,即
,即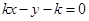 ,
,圆心
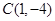 到直线
到直线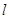 的距离
的距离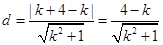 ,
,设
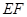 的中点为
的中点为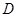 ,连接
,连接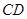 ,则必有
,则必有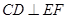 ,
,在
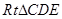 中,
中,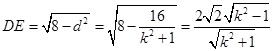 ,所以
,所以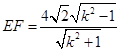 ,
,而原点到直线的距离为
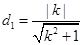 ,所以
,所以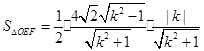
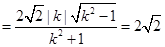 ,
,整理,得
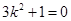 ,不存在这样的实数
,不存在这样的实数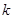 ,
,综上所述直线的方程为
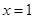 .
.
练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为 为参数),圆
为参数),圆 的极坐标方程为
的极坐标方程为 .
. 对称,求
对称,求 的值;
的值; +
+ 与
与 共线?如果存在,求k的值;如果不存在,请说明理由.
共线?如果存在,求k的值;如果不存在,请说明理由. 与圆
与圆 相交所得的弦的长为( )
相交所得的弦的长为( )



 与圆
与圆 相交于
相交于 两点,且
两点,且 (其中
(其中 为原点),则
为原点),则 的值为( )
的值为( )

 或
或 或
或 与
与 的交点分别为
的交点分别为 、
、 ,则
,则 .
.  与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以
与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以 为半径的圆与直线l相切,则△AOB面积为_____________.
为半径的圆与直线l相切,则△AOB面积为_____________. 在曲线
在曲线 (
( 为参数,
为参数, )上,则
)上,则 的取值范围是 .
的取值范围是 . 满足
满足 ,则
,则 的最小值是( )
的最小值是( )


