题目内容
已知-
≤x≤
,f(x)=tan2x+2tanx+2,求f(x)的最值及相应的x值.
| π |
| 3 |
| π |
| 4 |
考点:复合三角函数的单调性
专题:三角函数的求值
分析:换元法,令tanx=t,可得t的范围,可得关于t的二次函数,由二次函数区间的最值求法可得.
解答:
解:∵-
≤x≤
,∴-
≤tanx≤1,
令tanx=t,则-
≤t≤1,
∴f(x)=tan2x+2tanx+2可化为y=t2+2t+2=(t+1)2+1,
由二次函数的性质可得当t∈[-
,-1]时函数y单调递减,
当t∈[-1,1]时函数y单调递增,
∴当t=-1即x=-
时,y取最小值1,
当t=1即x=
时,y取最大值5
| π |
| 3 |
| π |
| 4 |
| 3 |
令tanx=t,则-
| 3 |
∴f(x)=tan2x+2tanx+2可化为y=t2+2t+2=(t+1)2+1,
由二次函数的性质可得当t∈[-
| 3 |
当t∈[-1,1]时函数y单调递增,
∴当t=-1即x=-
| π |
| 4 |
当t=1即x=
| π |
| 4 |
点评:本题考查复合三角函数的单调性,涉及二次函数和正切函数的性质,属中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知向量
、
是平面α内的两个不相等的非零向量,非零向量
在直线l上,则
•
=0,且
•
=是l⊥α的( )
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
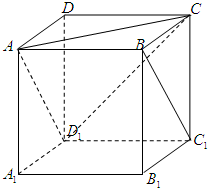 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: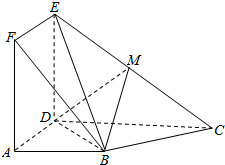 正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=