题目内容
14．△ABC中已知cosA•sinB＜0，试确定△ABC的形状．分析 利用三角函数的定义和符号之间的关系即可得到结论．
解答 解：在三角形中，sinB＞0，
由sinB•cosA＜0得cosA＜0，即$\frac{π}{2}$＜A＜π，
故三角形是钝角三角形．
点评 本题主要考查三角形形状的判断，根据三角函数的取值符号是解决本题的关键，比较基础．
练习册系列答案
相关题目
4．已知集合A={x|x＜-2}，B={x|x2＞4}，则“x∈A”是“x∈B”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
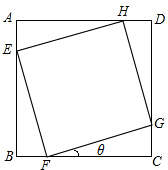如图所示，某住宅小区内有一正方形草地ABCD，现欲在其中修建一个正方形花坛EFGH，若已知花坛面积为正方形草地面积的$\frac{2}{3}$，则θ=arctan（2-$\sqrt{3}$）．
3．下列不等式中成立的是（ ）
| A． | sin140°＜sin30° | B． | cos140°＜cos130° | C． | tan40°＜tan30° | D． | sin40°＜sin30° |