题目内容
5.已知抛物线C:y2=4x焦点为F,直线MN过焦点F且与抛物线C交于M,N两点,P为抛物线C准线l上一点且PF⊥MN,连接PM交y轴于Q点,过Q作QD⊥MF于点D,若|MD|=2|FN|,则|MF|=$\sqrt{3}$+2.分析 直线MN的方程为y=k(x-1),代入抛物线方程可得k2x2-(2k2+4)x+k2=0,求出k的值可得M的坐标,即可得出结论.
解答 解:设M(x1,y1),N(x2,y2),直线MN的方程为y=k(x-1),代入抛物线方程可得k2x2-(2k2+4)x+k2=0
∴x1+x2=2+$\frac{4}{{k}^{2}}$,
2|FN|=|MD|,可得2(x2+1)=|MD|,
∵$\frac{MD}{MF}=\frac{MQ}{MP}$,∴$\frac{2({x}_{2}+1)}{{x}_{1}+1}$=$\frac{{x}_{1}}{{x}_{1}+1}$,∴x2=$\frac{1}{2}{x}_{1}$-1,
联立可得x1=2+$\frac{8}{3{k}^{2}}$,
∵x1=$\frac{{k}^{2}+2+2\sqrt{1+{k}^{2}}}{{k}^{2}}$,
∴2+$\frac{8}{3{k}^{2}}$=$\frac{{k}^{2}+2+2\sqrt{1+{k}^{2}}}{{k}^{2}}$,
∴3k2=4$\sqrt{3}$+4,
∴x1=$\sqrt{3}$+1,
∴|MF|=$\sqrt{3}$+2,
故答案为$\sqrt{3}$+2.
点评 本题考查抛物线的方程与性质,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
16.如图,某几何体的三视图如图所示,则该几何体的各条棱中最长的棱和最短的棱长度之和为( )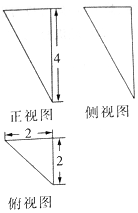

| A. | 6 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{5}$+2 | D. | 2$\sqrt{6}$+2 |
16.已知集合U={1,2,3,4,5,6}M={1,2},N={2,3,4},则M∩(∁UN)=( )
| A. | {1} | B. | {2} | C. | {1,2,5,6} | D. | {1,2,3,4} |
20.已知集合 A={x|x2<4},B={0,1,2,3},则A∩B=( )
| A. | ∅ | B. | {0} | C. | {0,1} | D. | {0,1,2} |
17.设f′(x)、g′(x)分别是函数f(x)、g(x)(x∈R)的导数,且满足g(x)>0,f′(x)g(x)-f(x)g′(x)>0.若△ABC中,∠C是钝角,则( )
| A. | f(sinA)•g(sinB)>f(sinB)•g(sinA) | B. | f(sinA)•g(sinB)<f(sinB)•g(sinA) | ||
| C. | f(cosA)•g(sinB)>f(sinB)•g(cosA) | D. | f(cosA)•g(sinB)<f(sinB)•g(cosA) |
11.已知圆C:(x-1)2+y2=r2(r>0).设条件p:0<r<3,条件q:圆C上至多有2个点到直线x-$\sqrt{3}$y+3=0的距离为1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |