题目内容
10.已知数列{an}的前n项和为Sn,满足:a1=1,${S_{n+1}}-{S_n}=\frac{3^n}{a_n}(n∈{N^*})$,则该数列的前2017项和S2017=31009-2.分析 由a1=1,${S_{n+1}}-{S_n}=\frac{3^n}{a_n}(n∈{N^*})$,可得an+1an=3n,n=1时,a2=3.n≥2时,anan-1=3n-1,可得$\frac{{a}_{n+1}}{{a}_{n-1}}$=3.因此数列{an}的奇数项与偶数项都成等比数列,公比为3.即可得出.
解答 解:∵a1=1,${S_{n+1}}-{S_n}=\frac{3^n}{a_n}(n∈{N^*})$,∴an+1an=3n,n=1时,a2=3.
n≥2时,anan-1=3n-1,可得$\frac{{a}_{n+1}}{{a}_{n-1}}$=3.
∴数列{an}的奇数项与偶数项都成等比数列,公比为3.
∴S2017=(a1+a3+…+a2017)+(a2+a4+…+a2016)
=$\frac{{3}^{1009}-1}{3-1}$+$\frac{3({3}^{1008}-1)}{3-1}$=31009-2.
故答案为:31009-2.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、分组求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设p:2x<1,q:x(x+1)<0,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知集合M={x|0<x<3},N={x|x>2},则M∩(∁RN)=( )
| A. | (0,2] | B. | [0,2) | C. | (2,3) | D. | [2,3) |
15.半径为2的圆C的圆心在第四象限,且与直线x=0和$x+y=2\sqrt{2}$均相切,则该圆的标准方程为( )
| A. | (x-1)2+(y+2)2=4 | B. | (x-2)2+(y+2)2=2 | C. | (x-2)2+(y+2)2=4 | D. | (x-2$\sqrt{2}$)2+(y+2$\sqrt{2}$)2=4 |

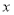 ,
,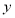 满足约束条件
满足约束条件 若
若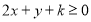 恒成立,则实数
恒成立,则实数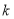 的取值范围为 .
的取值范围为 .