题目内容
15.设集合A={a1,a2,…,an}(其中ai∈R,i=1,2,…,n),a0为常数,定义:ω=$\frac{1}{n}$[sin2(a1-a0)+sin2(a2-a0)+…+sin2(an-a0)]为集合A相对a0的“正弦方差”,则集合{$\frac{π}{2}$,π}相对a0的“正弦方差”为$\frac{1}{2}$.分析 直接利用新定义,列出关系式求解即可.
解答 解:设集合A={a1,a2,…,an}(其中ai∈R,i=1,2,…,n),a0为常数,
定义:ω=$\frac{1}{n}$[sin2(a1-a0)+sin2(a2-a0)+…+sin2(an-a0)]为集合A相对a0的“正弦方差”,
则集合$\left\{{\frac{π}{2},π}\right\}$相对a0的“正弦方”为:$\frac{1}{2}$(sin2($\frac{π}{2}$-a0)+sin2(π-a0))=$\frac{1}{2}$(cos2a0+sin2a0)=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 本题考查新定义的应用,三角函数的化简求值,考查计算能力.

练习册系列答案
相关题目
5.若关于x的不等式sin(x+1)≤ax+a的解集为[-1,+∞),则a的取值范围为( )
| A. | [$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (0,+∞) | D. | [1,+∞) |
3.已知函数f(x)=cosωx-sinωx(ω>0)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,则ω的取值不可能为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
20.已知直线y=m(0<m<2)与函数f(x)=2sin(ωx+φ)(ω>0)的图象相邻的三个交点依次为A(1,m),B(5,m),C(7,m),则ω=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
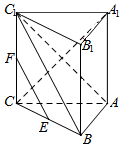 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.