题目内容
14.如图,在正方形ABCD中,AD=4,E为DC上一点,且$\overrightarrow{DE}$=3$\overrightarrow{EC}$,则$\overrightarrow{AB}$•$\overrightarrow{AE}$( )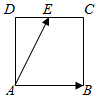
| A. | 20 | B. | 16 | C. | 15 | D. | 12 |
分析 由题意把$\overrightarrow{AE}$用$\overrightarrow{AB}、\overrightarrow{AD}$表示,代入$\overrightarrow{AB}$•$\overrightarrow{AE}$,展开后由向量的数量积运算得答案.
解答 解:∵ABCD为边长是4正方形,∴$\overrightarrow{AB}•\overrightarrow{AD}=0$,
∵$\overrightarrow{DE}$=3$\overrightarrow{EC}$,
∴$\overrightarrow{DE}=\frac{3}{4}\overrightarrow{DC}=\frac{3}{4}\overrightarrow{AB}$,
∴$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AD}+\frac{3}{4}\overrightarrow{AB}$,
则$\overrightarrow{AB}$•$\overrightarrow{AE}$=$\overrightarrow{AB}•(\overrightarrow{AD}+\frac{3}{4}\overrightarrow{AB})=\overrightarrow{AB}•\overrightarrow{AD}+\frac{3}{4}|\overrightarrow{AB}{|}^{2}$=$\frac{3}{4}×{4}^{2}=12$.
故选:D.
点评 本题考查平面向量的数量积运算,考查了向量加法的三角形法则,是中档题.

练习册系列答案
相关题目
4.已知实数a,b,c满足a>b>c,则下列结论正确的是( )
| A. | ac>bc | B. | ac>bc | C. | ca>cb | D. | 2a>2b |
5.若关于x的不等式sin(x+1)≤ax+a的解集为[-1,+∞),则a的取值范围为( )
| A. | [$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (0,+∞) | D. | [1,+∞) |
19.已知全集为R,集合M={-1,1,2,4},N={x|x2-2x>3},则M∩(∁RN)=( )
| A. | {-1,1,2} | B. | {1,2} | C. | {4} | D. | {x|-1≤x≤2} |
3.已知函数f(x)=cosωx-sinωx(ω>0)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,则ω的取值不可能为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
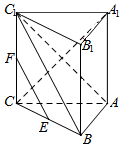 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.