题目内容
点P(a,b)在函数y=
x-x2的图象上运动,则
的取值范围是 .
| 2 |
| b-2 |
| a-3 |
考点:直线的斜率
专题:计算题,函数的性质及应用,不等式的解法及应用,空间位置关系与距离
分析:设b-2=k(a-3),由b=
a-a2,从而可得:a2+a(k-
)+2-3k=0,故△=a(k-
)2-4(2-3k)=k2+k(12-2
)-6≥0.从而解得
的取值范围.
| 2 |
| 2 |
| 2 |
| 2 |
| b-2 |
| a-3 |
解答:
解:设b-2=k(a-3),①
由b=
a-a2,②
从而可得:k(a-3)+2=
a-a2,
整理有:a2+a(k-
)+2-3k=0,
故△=a(k-
)2-4(2-3k)=k2+k(12-2
)-6≥0.
从而解得:k≥
-6+2
或≤
-6-2
.
故答案为:[-∞,
-6+2
]∪[
-6-2
,+∞].
由b=
| 2 |
从而可得:k(a-3)+2=
| 2 |
整理有:a2+a(k-
| 2 |
故△=a(k-
| 2 |
| 2 |
从而解得:k≥
| 6 |
11-3
|
| 6 |
11-3
|
故答案为:[-∞,
| 6 |
11-3
|
| 6 |
11-3
|
点评:本题主要考查了不等式的解法及应用,函数的性质及应用,空间位置关系与距离,考查了转化思想,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知函数f(x)=
-logax的零点为x1,函数g(x)=
-ax的正零点为x2,其中a>0且a≠1,m>1,则下列选项一定正确的是( )
| m-x2 |
| m-x2 |
| A、x12+x22=m |
| B、x1>x2 |
| C、x1<x2 |
| D、x12+x22的值与a值有关 |
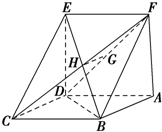 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.四棱锥F-ABCD的体积的最大值( )
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.四棱锥F-ABCD的体积的最大值( )| A、4 | ||
B、
| ||
C、
| ||
| D、2 |
已知f(x)=x3+2x,则f(5)+f(-5)的值是( )
| A、0 | B、-1 | C、1 | D、2 |