题目内容
10.已知函数f(x)=x-(a+1)lnx-$\frac{a}{x}$,其中a∈R.(Ⅰ)求证:当a=1时,函数y=f(x)没有极值点;
(Ⅱ)求函数y=f(x)的单调增区间.
分析 (Ⅰ)求出函数的导数,根据导函数的符号,求出函数的单调区间,证明结论即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可.
解答 (Ⅰ)证明:函数f(x)的定义域是(0,+∞).
当a=1时,f(x)=x-2lnx-$\frac{1}{x}$,
函数f′(x)=$\frac{{(x-1)}^{2}}{{x}^{2}}$≥0,
所以函数f(x)在定义域(0,+∞)上单调递增,
所以当a=1时,函数y=f(x)没有极值点;
(Ⅱ)f′(x)=1-$\frac{a+1}{x}$+$\frac{a}{{x}^{2}}$=$\frac{(x-1)(x-a)}{{x}^{2}}$,x∈(0,+∞)
令f′(x)=0,得x1=1,x2=a,
①a≤0时,由f′(x)>0可得x>1,
所以函数f(x)的增区间是(1,+∞);
②当0<a<1时,由f′(x)>0,可得0<x<a,或x>1,
所以函数f(x)的增区间是(0,a),(1,+∞);
③当a>1时,由f′(x)>0可得0<x<1,或x>a,
所以函数f(x)的增区间是(0,1),(a,+∞);
④当a=1时,
由(Ⅰ)可知函数f(x)在定义域(0,+∞)上单调递增.
综上所述,当a≤0时,函数y=f(x)的增区间是(1,+∞);
当0<a<1时,所以函数f(x)的增区间是(0,a),(1,+∞);
当a=1时,函数f(x)在定义域(0,+∞)上单调递增;
当a>1时,所以函数f(x)的增区间是(0,1),(a,+∞).
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
20.在△ABC中,点D满足$\overrightarrow{BC}$=3$\overrightarrow{BD}$,则( )
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ |
15.已知函数f(x)=2x+x-4,g(x)=ex+x-4,h(x)=lnx+x-4的零点分别是a,b,c,则a,b,c的大小顺序是( )
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | c<a<b |
 如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.
如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.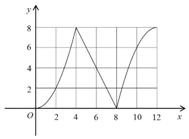 如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:
如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空: