题目内容
2．观察下列式子：13=1，23=3+5，33=7+9+11，43=13+15+17+19，…，按照上述规律，则83=57+59+61+63+65+67+69+71．
分析 观察可看出：观察题目等式可知，第8个等式的右边是8个连续的奇数之和，所以可以逐行写出，最终可求得结果．
解答 解：观察题目等式可知，第8个等式的右边是8个连续的奇数之和，
13=1
23=3+5，
33=7+9+11，
43=13+15+17+19，
53=21+23+25+27+29，
63=31+33+35+37+39+41，
73=43+45+47+49+51+53+55，
83=57+59+61+63+65+67+69+71，
故答案为：57+59+61+63+65+67+69+71
点评 这是一道考查归纳推理的问题，一般是根据前面的几项（或式子），找出一般性的规律，然后再对所求的情况求解，本题因为8不大，所以可以采用列举法．
练习册系列答案
阅读快车系列答案
相关题目
17．
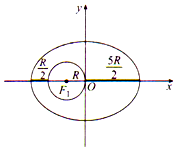我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）| A． | $\frac{2}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |
11．定义在[0，+∞）上的函数f（x），当x∈[0，2]时，f（x）=4（|x-1|-1），且对任意实数 x∈[2n-2，2n+1-2]（n∈N*，n≥2），都有f（x）=$\frac{1}{2}$f（$\frac{x}{2}$-1），若方程f（x）-log a x=0有且仅有三个实根，则实数a的取值范围是（ ）
| A． | [$\frac{\sqrt{10}}{10}$，$\frac{\sqrt{2}}{2}$） | B． | （$\frac{\sqrt{10}}{10}$，$\frac{\sqrt{2}}{2}$） | C． | （$\frac{1}{10}$，$\frac{1}{2}$） | D． | [$\frac{1}{10}$，$\frac{1}{2}$） |