题目内容

已知数列{an}的通项公式an=7n+2，数列{bn}的通项公式bn=lgan，证明：数列{bn}是等差数列．
考点：等差关系的确定
专题：等差数列与等比数列
分析：把数列{an}的通项公式an=7n+2代入bn=lgan，然后直接利用等差数列的定义证明．
解答： 证明：由an=7n+2，得bn=lgan=lg7n+2=（n+2）lg7，
则bn+1=（n+3）lg7，
∴bn+1-bn=（n+3）lg7-（n+2）lg7=lg7．
∴数列{bn}是等差数列．
点评：本题考查了等差关系的确定，考查了对数式的运算性质，是基础题．
练习册系列答案
相关题目
在△ABC中，角A，B，C对边分别是a，b，c，满足2
AB
•
AC
=a2-(b+c)2．
（1）求角A的大小；
（2）求sinA•sinB•sinC的最大值，并求取得最大值时角B，C的大小．
已知全集U={1，2，3，4，5}，A={1，2，4}，B={2，5}，则（∁UA）∪B=（　　）
A、{3，4，5}
B、{2，3，5}
C、{5}
D、{3}
已知θ为锐角且
cos3θ
cosθ
=
1
3
，则
sin3θ
sinθ
=
 
．
已知A，B，C，D是球O表面上的点，AB，AC，AD两两垂直，△ABC，△ACD，△ADB的面积分别为
2
2
，
3
2
，
6
2
，则球O的表面积为
 
．
已知函数f（x）的部分图象如图所示，则下列关于f（x）的表达式中正确的是（　　）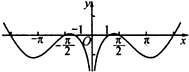
A、f（x）=
sinx
x2
B、f（x）=（lnx）cos2x
C、f（x）=（ln|x|）sin2x
D、f（x）=（ln|x|）cosx
若关于x的方程2cos2（π+x）-sinx+a=0有实根，求实数a的取值范围．
在等差数列{an}中，S10=100，S20=110，则S40的值为
 
．
设i是虚数单位，复数 Z=1+
1-i
1+i
为（　　）
A、1+iB、1-i
C、C、-1+iD、-1-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网