题目内容
求函数y=2sin（2x+
）+1的增区间．
| π |
| 3 |
考点：正弦函数的单调性
专题：三角函数的图像与性质
分析：根据条件利用正弦函数的单调增区间，求出函数的递增区间即可得到结论．
解答：
解：∵y=2sin（2x+
）+1，
∴由2kπ-
≤2x+
≤2kπ+
，k∈Z．
得kπ-
≤x≤kπ+
，k∈Z．
∴函数的单调递增区间为[kπ-
，kπ+
]，k∈Z．
| π |
| 3 |
∴由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得kπ-
| 5π |
| 12 |
| π |
| 12 |
∴函数的单调递增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
点评：本题主要考查正弦函数的单调性的应用，要求熟练掌握三角函数的图象和性质．
练习册系列答案
相关题目
设集合A={α|α=k•180°+90°，k∈z}∪{α|α=k•180°，k∈z}，集合B={β|β=k•90°，k∈z}，则（ ）
| A、A?B | B、A?B |
| C、A∩B=∅ | D、A=B |
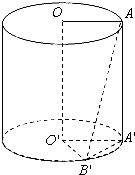圆柱的高为4cm，底面半径为3cm，上底面一条半径OA与下底面一条半径O′B′成60°角，求：