Question

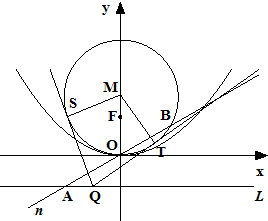已知抛物线C：x²=2py（p＞0）的准线为L，焦点为F，⊙M的圆心在y轴的正半轴上，且与x轴相切，过原点作倾斜角为

π

6

的直线n，交L于点A，交⊙M于另一点B，且|AO|=|OB|=2
（Ⅰ）求⊙M和抛物线C的方程；
（Ⅱ）过L上的动点Q作⊙M的切线，切点为S、T，求当坐标原点O到直线ST的距离取得最大值时，四边形QSMT的面积．

Answer 1

考点：圆与圆锥曲线的综合

专题：圆锥曲线中的最值与范围问题

分析：（Ⅰ）画出图形，设准线交y轴于N，在直角三角形ANO中，结合已知条件求出|ON|即p的值，则抛物线方程可求，在三角形MOB中，由三角形为正三角形得到|OM|的值，从而求得圆的方程；
（Ⅱ）设出两个切点的坐标，求出两条切线的方程，进一步得到ST所在直线方程，写出原点到ST的距离，分析可知当a=0时即Q在y轴上时原点到ST的距离最大，由此求出ST与MQ的长度，则四边形QSMT的面积可求．

解答： 解：（Ⅰ）如图，

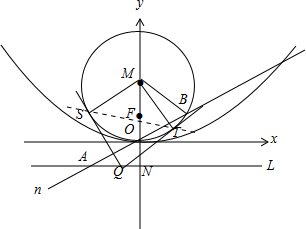
设准线L交y轴于N(0，-

p

2

)，在Rt△OAN中，∠OAN=

π

6

，
∴|ON|=

|OA|

2

=1，
∴p=2，则抛物线方程是x²=4y；
在△OMB中有OM=OB，∠MOB=

π

3

，
∴OM=OB=2，
∴⊙M方程是：x²+（y-2）²=4；
（Ⅱ）设S（x₁，y₁），T（x₂，y₂），Q（a，-1）
∴切线SQ：x₁x+（y₁-2）（y-2）=4；切线TQ：x₂x+（y₂-2）（y-2）=4，
∵SQ和TQ交于Q点，
∴ax₁-3（y₁-2）=4和ax₂-3（y₂-2）=4成立，
∴ST方程：ax-3y+2=0．
∴原点到ST距离d=

2

a2+9

，当a=0，即Q在y轴上时d有最大值．
此时直线ST方程是y=

2

3

．
代入x²+（y-2）²=4，得x=±

2 5

3

．
∴|ST|=

4 5

3

，|MQ|=3．
此时四边形QSMT的面积S=

1

2

×

4 5

3

×3=2

5

．

点评：本题主要考查圆与圆锥曲线的综合问题，其中涉及到抛物线以及圆的标准方程的求法，考查了圆的切线方程的求法及过圆切点的直线方程的求法，综合考查了学生分析问题的能力和基础的运算能力，是有一定难度题目．