题目内容
函数f(x)=cos(2x-
)+1的对称中心为 .
| π |
| 6 |
考点:余弦函数的对称性
专题:三角函数的图像与性质
分析:根据余弦函数的性质即可求出函数的对称中心.
解答:
解:由2x-
=
+kπ,解得x=
+
,k∈Z,
即函数y=cos(2x-
)的对称中心为(
+
,0),k∈Z,
则函数f(x)=cos(2x-
)+1的对称中心为(
+
,1),k∈Z,
故答案为:(
+
,1),k∈Z.
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| kπ |
| 2 |
即函数y=cos(2x-
| π |
| 6 |
| π |
| 3 |
| kπ |
| 2 |
则函数f(x)=cos(2x-
| π |
| 6 |
| π |
| 3 |
| kπ |
| 2 |
故答案为:(
| π |
| 3 |
| kπ |
| 2 |
点评:本题主要考查三角函数的对称中心,要求熟练掌握三角函数的图象和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
两条平行线3x-4y+1=0与6x-8y-2=0之间的距离为( )
A、
| ||
| B、2 | ||
C、
| ||
D、
|
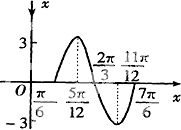 已知函数y=Asin(ωx+φ)(|φ|<
已知函数y=Asin(ωx+φ)(|φ|<