题目内容
若函数y=x•e2x，则此函数的导数y′= ．
考点：导数的运算
专题：导数的概念及应用
分析：根据函数的导数公式进行计算即可得到结论．
解答：
解：∵y=x•e2x，
∴y′=e2x+x•（e2x）′=e2x+2x•（e2x）=（2x+1）e2x，
故答案为：（2x+1）e2x
∴y′=e2x+x•（e2x）′=e2x+2x•（e2x）=（2x+1）e2x，
故答案为：（2x+1）e2x
点评：本题主要考查函数的导数计算，要求熟练掌握常见函数的导数公式．
练习册系列答案
阅读快车系列答案
相关题目
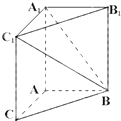如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．
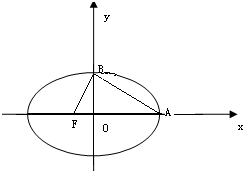已知双曲线的中心在坐标原点，焦点在x轴上，A是右顶点，B是虚轴的上端点，F是左焦点，当BF⊥AB时，此类双曲线称为“黄金双曲线”，其离心率为e=